The B_s meson is a particle made up by a bottom quark and a anti-strange quark (or the opposite: a anti-bottom and a strange quark; the two states are not distinguished in the decay mode we study here). While heavy and fancy -since it contains a bottom quark, a particle not present in ordinary matter- the B_s is not really an exceedingly interesting particle to study in the 21st century: we have studied it in great detail in the course of the past twenty years at hadron and lepton colliders, and we know basically everything that there is to know about it. However...
The fact is, the B_s is a neutral meson made up by two different quarks. Such particles have a tradition of being an open door to increasing our knowledge in the subatomic world, as exemplified by the various advancements we made by studying the K0 meson - a particle made up by a down and antistrange quark, so quite similar (except for its mass) to the B_s.
In particular, by studying the K0 meson, physicists in the sixties of last century realized that there had to be some mechanism at work that ought to prevent the decay to a pair of leptons, such as in K0->μμ. That decay was not seen, while simple-minded reasoning in analogy with the copious decay of the K+ meson (made by a up-antistrange quark combination) into μν pairs impled one should find it copiously.
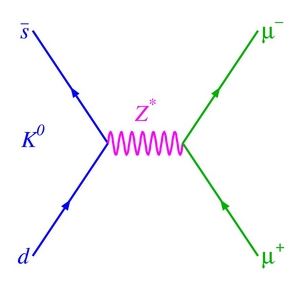 It appeared that while the charged-current weak interaction naturally coupled quarks of different flavour, and thus allowed the tree-level transmutation of a up-antistrange pair present in the K^+ meson into a positive-charged W meson, which then decayed into the muon-neutrino pair, the similar process in the K0 case was disallowed: flavor-changing neutral currents (FCNC) are null in the standard model at tree level, since the Z0 boson (the neutral counterpart of the W) is unable to do the same trick that the W ordinarily performs (see the impossible diagram on the right).
It appeared that while the charged-current weak interaction naturally coupled quarks of different flavour, and thus allowed the tree-level transmutation of a up-antistrange pair present in the K^+ meson into a positive-charged W meson, which then decayed into the muon-neutrino pair, the similar process in the K0 case was disallowed: flavor-changing neutral currents (FCNC) are null in the standard model at tree level, since the Z0 boson (the neutral counterpart of the W) is unable to do the same trick that the W ordinarily performs (see the impossible diagram on the right).Nowadays we know inside out all the details of allowed and disallowed standard model decays, and we can compute with high precision the rate of decay of the B_s meson into muon pairs: this is predicted to occur 3.52 times in a billion, thanks to particle reaction diagrams more complicated than tree-level ones (such as the K+ decay into μν, which one draws by simply collapsing into one point the down and anti-strange quark lines, emitting a single line, the W, which then bifurcates into the μν pair).
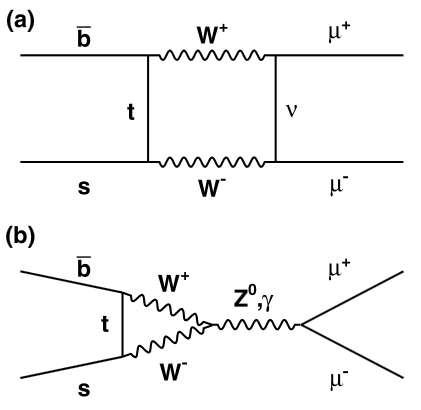 Note two things: One - this process is quite rare!, and Two - it exists only through the exchange of more than one intermediate particle; these intermediate states produce "loops". Example of possible diagrams for the decay of the B_s in two muons are shown on the left.
Note two things: One - this process is quite rare!, and Two - it exists only through the exchange of more than one intermediate particle; these intermediate states produce "loops". Example of possible diagrams for the decay of the B_s in two muons are shown on the left. In the diagram labeled "(a)" the two quark lines from the B_s enter from the left. The simultaneous emission of two W bosons change the b-quark into a top quark on the upper left vertex, and allow the absorption of the same by the s-quark line on the lower left vertex. The two W bosons then decay each into a muon-neutrino pair, when the neutrino remains an internal line. A "box" is thus formed.
In the diagram labeled "(b)" we witness a different process. The left part is the same; however, the two W bosons then merge into a Z, and it is the latter which turns into the two muons. Both diagrams are "second-order" weak processes, since they both include four vertex (as opposed to two vertex which are normally all it takes for a two-into-two reaction). Since each vertex implies "paying" a certain small probability (which depends on the strength of the coupling constant involved in the transmutation taking place), diagrams with more vertices are more rare!
The fact that the standard model predicts a very small rate for the B_s decay to dimuon pairs, coupled to the quite easy experimental signature that two muons provide, means that this is a very proficuous way to test the standard model: It is in fact quite nice to measure something very close to zero. Find a signal larger than the ridiculously low predicted rate, and you are done - new physics!
But the above would be a really generic motivation. Instead, the fact that the decay occurs through quantum loops means that indeed any -even very heavy- new particle, not predicted by the standard model, could contribute measurably to the decay rate. In particular, supersymmetric particles would, in most versions of SUSY, enhance considerably the rate of the process !
Because of the above - the chance of indirecly discovering very heavy SUSY particles through the study of a low-energy process- the search for B_s decays to muon pairs has been performed with great care in all past experiments producing large numbers of such particles. You well realize, however, that in order to be sensitive to the predicted standard model decay rate, 3 in a billion, you need to produce billions of B_s mesons. Until recently, this was not possible, but now the LHC luminosity allowed us to reach that goal.
First came the LHCb experiment, which is well-suited for this search - it "looks" in the forward direction of proton-proton collisions, where many B mesons are produced. However, LHCb could see only a 3.5 sigma signal of B_s mesons in their latest analysis. A signal perfectly compatible with the standard model prediction, but not large enough to be a foul-proof observation.
The news of today is that the CMS experiment has analyzed 25 inverse femtobarns of collisions, and has extracted a more significant signal of B_s decays: the signal stands at 4.3 standard deviations above backgrounds. Note that this is not yet above the "5-sigma" mark, but as I have noted several times in the past, that psychological threshold is a convention that applies well to new particle claims, while here we are just measuring a process we know must exist. The CMS publication is positive in its claims: already in the Abstract it says
"An excess of B_s -> μμ events with respect to backgrounds is observed with a significance of 4.3 standard deviations"
which is different from saying, as one would have probably done for a new particle, "An excess of events, compatible with the X --> yy hypothesis, is observed...".
With their data fits, CMS determines the branching fraction in the observed decay mode to be 3.0+1.0-0.9 billionths, which is in great agreement with the standard model alone. This measurement will no doubt be used by phenomenologists to further restrict the allowed parameter space of SUSY theories, since many combinations of SUSY parameters would predict the B_s decay to muon pairs to be several times larger than what is measured by CMS.
The figure below shows two mass distributions for muon pairs; they refer to alternative multivariate data selection strategies, based on boosted decision trees of different complexity. The default result is the one on the left, yielding a signal with a significance of 4.3 standard deviations; the result on the right instead, based on a more stringent BDT selection, produces a signal with a significance of 4.8 standard deviations. Note that the default selection is the one which should have produced the most significant result (expectation was 4.8 sigma, against 4.7 of the BDT method resulting in the distribution on the right)... Statistics plays these tricks now and then.
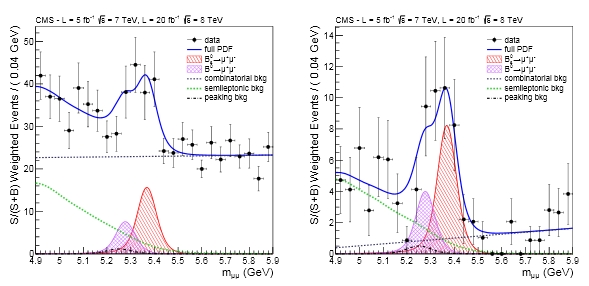
Also worth noting is that the data in the histograms is weighted by the expected signal to noise fraction, which varies across different categories (most notably, the polar angle of the muons, which makes them cross different detector elements and causes backgrounds to differ).
The fits above allow for backgrounds as well as two distinct signals, one of the B_s meson (in red) and one for the B_d meson (in blue), which I have avoided discussing so far. Maybe a few words on that meson are also needed now!
While the B_s is made up by a bottom-antistrange combination, the B_d is made up by a bottom-antidown quark pair. The down quark is lighter than the strange quark, so the B_d is lighter than the B_s. Details of the quantum loops producing the rare dimuon decay make the probability that a B_d turns into two muons even smaller (thirty times more so) than the one for the B_s. So with the available statistics we would not expect to observe that decay as well; however, it is of course reasonable to include the B_d signal in these mass fits: this allows to measure an upper limit for that process, too.
The B_d signal is not significant in the CMS data, and indeed CMS quotes an upper limit for the B_d -> μμ decay rate, at 1.1 billionths (at 95% confidence level). We are, in other words, still a factor of ten above the standard model rate here. Note that the B_d decay could also be enhanced by supersymmetric particles in the quantum loops, and in a different way from the B_s; so it is very interesting to continue looking for that, and measuring the relative rate. That will be the business best left for the 2015 run of the LHC.
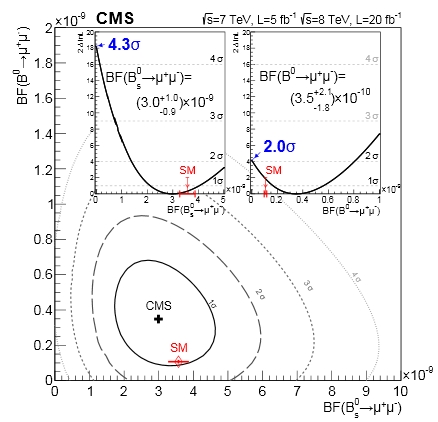
The last graph, shown above, is more technical than a simple mass distribution. It shows the two-dimensional measurement of the two branching fractions together. The CMS measurement is labeled by the black dot, and the "one-sigma" contour is a black oval. The oval includes the standard model prediction for the two branching fractions, in red. The insets also show the likelihood profiles for the two separate measurements, which indicate that the significance of the B_s signal is indeed 4.3 sigma, while the significance of the B_d signal is 2.0 sigma. Note that we saw more B_d events than we should have, although only marginally so: the SM prediction is three times lower than our central value; however, as the inset shows, the difference in delta-log-likelihood equates to being just "one sigma" away...
UPDATE: See also the official statement by CMS on this measurement on the CMS site.
UPDATE: LHCb just presented their improved results, which bring their signal to 4.0 standard deviations... Still, CMS is the leader here :)
UPDATE: I stand corrected - LHCb in fact had a slightly better expected sensitivity to B_s than CMS, with 5.0 standard deviations expected. However, they also fluctuated low, by one full sigma, to 4.0 standard deviations, while CMS fluctuated low by only 0.5 sigma, from 4.8 expected to 4.3 observed. The result is that CMS has the most significant observed effect.




Comments