“Up until now, the various lawsuits filed against the LHC have faltered. But if the right kind of claim is filed in the proper court, a judge may soon have to face the question of whether an injunction might be needed to save the world.”Johnson continues by making the claim that it is not impossible that 'Groupthink', might have caused the thousands of physicists involved to “reach a worry-free outlook that is not justified by the facts”. He further states that scientific arguments alone, whilst all that matters in academic disputes, will not be enough to demonstrate the safety of the LHC:
“The question of whether the LHC is safe is not academic – it is a real-world question with the highest possible stakes. Evaluating the science from a real-world perspective, and understanding scientific work to be a fallible human enterprise, is not merely fair – where justice is concerned it is essential.”Ouch. A well-known demagogic strategy to undermine hard scientific arguments. First establish that scientific facts are scholarly or academic by nature, and then use the term 'academic' pejoratively as if it is the antonym to 'real-world'.
Let's see if we can give this concerned lawyer a 'real-world' perspective on the risks involved. Nothing 'academic'. Just empirical facts and a bit of well-established high-school level physics. Some simple order-of-magnitude estimations will allow any lawyer or judge who is not completely alien to empirical physics, to place the LHC black hole risk in its right place within the scheme of things.
How to build a black hole
What does it take to form a black hole? The straightforward answer is: a lot of mass. That is generally true, but mass is not a number that in itself specifies black hole formation risk. One can, at least in principle, form black holes with widely different sizes and masses.
FBH = c4/4
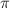 G = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 Newton.
G = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 Newton.That is not just a big number. That is a gigantic number specifying a truly supreme confinement. For comparison: the force that gravitationally confines Newton's apple to earth happens to be just 1 Newton.

How close to forming a black hole? Subatomic particle collisions (red) compared to mechanical presses (green), massive objects (blue) and gravitational systems (black). It takes 43 orders of magnitude to go from Newton's apple to a black hole.
Nutcrackers and particle smashers
How close can we get to a 1043 Newton confinement force? Let's say you need to crack open a nut, but you have no tools available. The best you can do is probably to place the nut in your mouth and crack it open using your bite. The human bite generates a surprisingly strong confinement force: about 700 Newton, comparable to the force needed to lift the same human in earth's gravitational field.
 With suitable tools you can do much better and generate a much larger confinement force. What you need is a tool that acts as force multiplier. A nutcracker fits the bill. But we have much more powerful force multipliers. The largest hydraulic presses available (beasts towering more than 20 meters high) generate confinement forces of about 50 kiloTons, or half a billion Newtons.
With suitable tools you can do much better and generate a much larger confinement force. What you need is a tool that acts as force multiplier. A nutcracker fits the bill. But we have much more powerful force multipliers. The largest hydraulic presses available (beasts towering more than 20 meters high) generate confinement forces of about 50 kiloTons, or half a billion Newtons.
Impressive, huh?
Maybe. But we can do even better. More than 10,000 times better.
A brute force approach (building larger hydraulic presses) will fail to realize confinement forces of such magnitude. We need to be a bit more clever and rethink the concept of confinement. Physics shows us the way: a confinement force corresponds to the ratio between the energy stored in the region, and the linear size of that region (for which we take the circumference that fits around the region):
Fconf = E / 2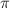 R
R
 So, a more clever way to generate high confinement forces is to increase the numerator and also decrease the denominator in this expression. For that we need to store a lot of energy in a small space. Particle smashers like the LHC excel at this task. However, they can't generate unlimited forces. According to quantum physics, the smallest circumference that can be achieved is inversely proportional to the energy:
So, a more clever way to generate high confinement forces is to increase the numerator and also decrease the denominator in this expression. For that we need to store a lot of energy in a small space. Particle smashers like the LHC excel at this task. However, they can't generate unlimited forces. According to quantum physics, the smallest circumference that can be achieved is inversely proportional to the energy:
2
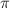 R
R 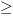 hc/E
hc/Ehere, h is Planck's constant, and c denotes the speed of light.
It follows that the confinement force can be made to scale with the square of the energy provided you manage to place that energy in the smallest possible volume:
Fconf  E2/hc
E2/hc
With collision energies in the LHC soon to reach 14 TeV (2 micro Joules) the LHC will be capable of cracking open subnuclear 'nuts' with forces that potentially can go up to 25 000 000 000 000 Newton (25 Tera Newton). That is a pretty impressive nut cracker!
However compared to the confinement force needed to create a black hole, the LHC falls short by almost thirty orders of magnitude. That is the same order of magnitude by which a grain of sand falls short of forming a volume as large as earth. I would tend to label that a pretty decent safety factor.
But there is more. Although impressive when compared to nutcrackers and hydraulic presses, LHC's confinement forces pale in significance when compared to ongoing uncontrolled particle smashings that no court will ever prohibit.
Oh-My-God!
 UHECRs are the high-energy particles that bombard us from outer space. Events with energies in excess of 1020 eV (more than ten million times the energy of the particles in the LHC) have been observed. Although at least fifteen similar events have been observed since, the 'Oh-My-God' particle observed in 1991 with the Fly's Eye detector array in Utah still holds the record. It did strike with a measured energy of 3 1020 eV (50 Joules). That is an energy capable of generating a confinement force of 13 000 000 000 000 000 000 000 000 000 Newton. That is close to a million times a billion larger confinement force than what can potentially be generated by the LHC. And the point is: these ultra-high energy cosmic rays hit earth at a rate of more than a million per year. Yet, even after billions of years of such bombardment, no black hole has swallowed earth. Not surprising at all, taken into account that the “Oh-My-God' confinement force, falls short from the force needed to create a black hole by a factor of a trillion. A decent safety factor, that made us survive millions times billions of events.
UHECRs are the high-energy particles that bombard us from outer space. Events with energies in excess of 1020 eV (more than ten million times the energy of the particles in the LHC) have been observed. Although at least fifteen similar events have been observed since, the 'Oh-My-God' particle observed in 1991 with the Fly's Eye detector array in Utah still holds the record. It did strike with a measured energy of 3 1020 eV (50 Joules). That is an energy capable of generating a confinement force of 13 000 000 000 000 000 000 000 000 000 Newton. That is close to a million times a billion larger confinement force than what can potentially be generated by the LHC. And the point is: these ultra-high energy cosmic rays hit earth at a rate of more than a million per year. Yet, even after billions of years of such bombardment, no black hole has swallowed earth. Not surprising at all, taken into account that the “Oh-My-God' confinement force, falls short from the force needed to create a black hole by a factor of a trillion. A decent safety factor, that made us survive millions times billions of events.
The black hole buzzing around your head
Have we any experience with confinement forces larger than the 'Oh-My-God confinement'? Sure we have.
 Force keeps matter together. Without confining forces, there would be no stable matter. How large are these confinement forces? That is easy. Let's start small and take a proton as an example. We again use the above energy/circumference formula to estimate the confinement force. For energy we substitute the rest energy (E = Mc2) and for a proton find a confinement force of 170 000 Newton. That is a number typical for the color confinement between quarks in nuclear particles like the proton.
Force keeps matter together. Without confining forces, there would be no stable matter. How large are these confinement forces? That is easy. Let's start small and take a proton as an example. We again use the above energy/circumference formula to estimate the confinement force. For energy we substitute the rest energy (E = Mc2) and for a proton find a confinement force of 170 000 Newton. That is a number typical for the color confinement between quarks in nuclear particles like the proton.
 What if we investigate larger massive objects? The confinement force, that scales with the mass/circumference ratio, will grow bigger. Let's take a housefly. The total confinement force that keeps a housefly together is about 40 000 000 000 000 Newton. Did you notice that this is slightly larger than the maximum confinement force that can be generated by the LHC? Impressive, right? Well, you might also turn the argument around and be disappointed by the feeble giant called LHC being defeated by a house fly when it comes to black-hole generating power.
What if we investigate larger massive objects? The confinement force, that scales with the mass/circumference ratio, will grow bigger. Let's take a housefly. The total confinement force that keeps a housefly together is about 40 000 000 000 000 Newton. Did you notice that this is slightly larger than the maximum confinement force that can be generated by the LHC? Impressive, right? Well, you might also turn the argument around and be disappointed by the feeble giant called LHC being defeated by a house fly when it comes to black-hole generating power.
 What about still larger masses? How large an object do we need to get a total confinement force compareable to that generated by the 'Oh-My-God' particle? That turns out to be an object somewhat bigger than a house fly, an object like '951 Gaspra', a piece of rock of 18 x 10 x 9 km in the asteroid belt of our solar system.
What about still larger masses? How large an object do we need to get a total confinement force compareable to that generated by the 'Oh-My-God' particle? That turns out to be an object somewhat bigger than a house fly, an object like '951 Gaspra', a piece of rock of 18 x 10 x 9 km in the asteroid belt of our solar system.
But we can still go further. What is the total confinement force of the earth itself? That force appears to reach a whopping 14 000 000 000 000 000 000 000 000 000 000 000 Newton. Huge. But not nearly enough to create a black hole. Still a safety margin of about a billion to go.
 Empirically we know that this safety factor is more than likely okay, if not indefinitely then at least for many, many millions of years to come. After all, we have the empirical evidence: earth has been around for a few billion years already. All that time it has been bombarded with many trillions 'Oh-My-God' events, yet so far earth hasn't shown any tendency of collapsing into a black hole.
Empirically we know that this safety factor is more than likely okay, if not indefinitely then at least for many, many millions of years to come. After all, we have the empirical evidence: earth has been around for a few billion years already. All that time it has been bombarded with many trillions 'Oh-My-God' events, yet so far earth hasn't shown any tendency of collapsing into a black hole.
In the meantime concerned lawyers can maybe entertain themselves with something more useful than hypothesizing frivolous lawsuits. What about filing restraining orders against the mini black holes buzzing around their heads?





Comments