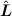Banner
    Unknown Physics Of Particle Orbital Momentum
    By Vladimir Kalitv... | January 4th 2011 06:51 AM | 19 comments | Print | E-mail | Track Comments
    More Articles
    All Articles
    About Vladimir

    Born in 1958 in Kharkov, USSR. Graduated from Kharkov State University in 1981 with major in Theoretical Nuclear Physics. Discovered positive charge...

    View Vladimir's Profile
    Everybody knows that the orbital momentum  is "quantized" and its z-projection  has integer eigenvalues in units of  . Too few, however, know that it is, in fact, a quasi-particle angular momentum which is integer-valued, not the particle one!

    To see it, let us consider two spinless particles with masses m1 and m2 coupled with any central potential, say, with 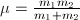 . The quasi-particle with the reduced mass  describes the relative particle motion and depends on both particles in a two-particle compound system. It is its orbital momentum which is quantized in terms of integer numbers, namely,  ranges from  to  .

    The particle-1 and particle-2 orbital (angular) momenta  and  , calculated relative to the system center of inertia, are just certain, generally non-integer fractions of  . 

    In particular, 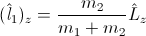    and 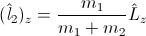  are not obliged to have integer values! Why? Because they are simply non-integer functions of operator  and are determined with its eigenvalues. For example, in the non-relativistic Positronium (where the particle masses are equal), if  , the electron orbital momentum  has the following values of projections: -1/2, 0, +1/2.

    Surprise! And the same statement is valid for the positron  projections in Positronium. "Half-integer" projections of a particle orbital momentum are thus possible and there is no kidding in it.

    The particle orbital momenta in a bound system with respect to the system center of inertia are not momenta of independent, non-correlated subsystems. On the contrary, they are related and the rule of addition of independent angular momenta, usually taught in courses of Quantum Mechanics, is not applicable to them.

    Comments

    I saw the discussion on Lubos' blog and of course agree with you. It's quite simple when one thinks in terms of relative coordinates and reduced masses. And your note makes it clear that the quantization only comes about due to what amounts to a sort of renormalization of the masses from particle masses to reduced masses.

    By the way, I think that arguing with people, especially Lubos, is a great idea. It sharpens the understanding.

    Carl Brannen (not verified) | 01/04/11 | 17:36 PM
    vongehr
    You can put any non-integer function of any quantized observable up, but the question is, are these observables? QM is not telling us about what 'is', but about what can be observed. Is there a measurement that finds these half integer orbital momenta? Since the minimum interaction is one action quantum h-bar, there should be a problem with bringing the electron from +1/2 down to 0 without bumping the positron's orbital momentum. The fundamental of all quantization in QM (i.e. not topological quantization like string winding numbers) is the fundamental quantization not of action, but of interaction (observation). Because h-bar is the fundamental interaction, angular momentum and spin measurements result in integer number differences.
    Sascha Vongehr | 01/04/11 | 23:03 PM
    Vladimir Kalitvianski
    Yes, many things are observable via observation of their functions. In our particular case, L is by definition is a sum of two angular momenta, so observing Lz means observing (l1)z and (l2)z "separately" because of unambiguous definition of L. This example shows that in an interacting system one often directly observes quasi-particle properties (oscillation frequencies, total masses, for example) rather than particle ones. It is very instructive to particle physicists who think they observe particle properties. In other words, I would say it is quasi-particles which are more fundamental in this, "observable" sense, not the particles. And it is not possible, of course, to flip the electron orbital momentum projection without influencing the positron's one - they are tightly related in this interacting system.

    P.S. In QFT there is an ambiguity of a "bare" constant and its "counter-term" because both are late human "inventions" to justify constant "renormalizations". It is not possible to figure out from their sum what the bare constant value is and what the counter-term value is. It is just postulated that their sum is always equal to the observable, given value. This "liberty" leads to an amusing thing - "renormalization group".
    Vladimir Kalitv... | 01/05/11 | 13:08 PM
    Vladimir Kalitvianski
    Alejandro wrote: "Can you link to your discussion in LM, to avoid redundancy of replies? In any case, what are the conjugate variables of l1 and l2? You should impose quantization on these, and then see if it is consistent or not. Particularly, which is the period of the conjugate variable? Is it a multiple of 2 pi?"

    Discussion in the Lubosh Motl's blog did not produce any advancement. For convenience of my readers, I prefer to repeat some explanations here.

    If you remember derivation of the Schroedinger equation for the relative distance r, you will see that it is constructed from r1 and r2 for which there are momenta operators p1 and p2, as well as the angular momenta operators l1 and l2. They obey the usual CCRs. In the reference frame where the whole system is at rest, the angular momenta operators l1 and l2 are proportional to each other, i.e., they are not independent. Factually, there is only one independent angular momentum operator. The "orbital" quantization is applied for their sum L, i.e., the periodicity in the "relative" angle . It is their mutual motion which should be periodical in the initial reference frame, if you like, to have an eigenstate for the whole system. It is especially evident for three and more bound particles.

    Again, it is quasi-particle properties that are quantized in the familiar sense, not particle ones! (And it has always been the case.)
    Vladimir Kalitv... | 01/05/11 | 17:54 PM
    Ah yes, in the reference frame where the whole system is at rest we can see things more clearly: we have changed variables (say, for the energy eigenfunction or for the total angular momentum eigenfunction, if both operators commute) from f(r1,r2) to f ( r2-r1, m1 r1 + m2 r2), and then we have set to zero the second variable. So there is a quantisation restriction or ligature, m1 r1 = - m2 r2, which must be taken in the quantum theory, and also when you decompose the "single variable" total eigenfunction f(r2-r1) as sum of products \sum g(r1) h(r2) of angular momentum eigenfunctions for particles 1 and 2. I'd enjoy to read a text doing this decomposition with the due care. If you produce one such text, please tell me.

    Alejandro Rivero (not verified) | 01/05/11 | 19:30 PM
    vongehr
    Not sure I am getting what you are getting at with "observing Lz means observing ... and ... 'separately'". Also, I am not sure what your stressing of 'pseudo-particles' is all about. Do you believe in some sort of true, real particles? With gravity being probably emergent and the world some sort of hologram in at least a valid dual description, all particles are pseudo-particles anyways. Fundamental physics is not about particles but about what observations can be made, what yes/no answers are decidable. I do not see how in this framework your 1/2 h-bar angular momentum is observable (= 'real').
    Sascha Vongehr | 01/06/11 | 03:48 AM
    Ladislav Kocbach
    I agree that this is not often realized, but it is not really unknown. Everybody knows it. More important is that to be able to "localize" the center of mass, you must "know" where the other particle is. This problem already occurred in the Einstein-Podolsky-Rosen paper, and it was nicely but not very clearly discussed away by N. Bohr in his "Reply". The conserved quantity is the "internal" angular momentum of the positronium, i.e. the angular momentum of the relative motion. Angular momenta of the two individual particles - electron and positron - have no special property - like conservation. This is true also in classical physics. To describe a physical system, we need to find coordinates which are meaningful. The individual angular momenta of two interacting isolated particles are simply not meaningful quantities. The case seems to be different for the charge distributions, as far as they can be related to other possibilities of measurement - and even there it would only be the expectation values. One can construct expectation values of anything - while finding eigenvalues is a different story. This last aspect is in fact already contained in the previous comment by Sascha Vongehr.
    Ladislav Kocbach | 01/05/11 | 06:39 AM
    Vladimir Kalitvianski
    In our particular case of two bound particles, both orbital momenta are conserved because they are proportional to a conserved orbital momentum of the whole system. They both are meaningful because it is they that determine the total angular momentum L. They both are "correlated" in a strong sense - they are proportional to each other. Collective, strongly correlated motion of atoms in a crystal lattice may be represented and observed as a sum of "independent" phonons but it does not make motion of one atom in the lattice meaningless. Such things are interchangeable. Knowing one thing makes it possible to know the other one and vice versa. All different variables are meaningful if they are expressed via reversible formulas. But not all variables are convenient for finding eigenstates. Normally, it is "separated" variables that are most convenient for the latter problem, however the complete solution (a superposition of states) is as complicated as the solution in "non-separated" variables.
    Vladimir Kalitv... | 01/06/11 | 03:49 AM
    It could be very useful if you can paint this in XIXth century mechanics. The equivalent question to the many particle case could be to ask how does the angular momentum (which is a conserved quantity under central forces, see Newton) become the "action unit" of the Lagrangian (for generic, no central, fields). If this is well understood, then the next steps, to classical field theory and to quantum mechanics, and then its union in QFT, could be easied to understand.

    Alejandro Rivero (not verified) | 01/05/11 | 16:30 PM
    Vladimir Kalitvianski
    Oh, I think quite differently: we should understand the classical mechanics proceeding from right constructions for QM and QFT which correspond better to the microscopic reality.
    Vladimir Kalitv... | 01/05/11 | 17:21 PM
    Ladislav Kocbach
    This is a comment on Vladimir's comment starting with: In our particular case of two bound particles, both orbital momenta are conserved because they are proportional to a conserved orbital momentum of the whole system....

    Indeed, both of the angular momenta with respect to the (common) center of mass are conserved (and they are "just" multiples of the relative angular momentum, so these "two" are in fact only one quantity , aren't they?). But there is no way to construct a single particle angular momentum, inependent of the other particle, since the angular momentum you are talking about is with respect to a center of mass, determined by the motion of the second particle. But do not worry, Einstein got this also more or less wrong in the EPR paper. I refer again to the N. Bohr's "Reply", but I am afraid you might force me to really read and interpret that argument. The old masters were not particularly clear in their discussions of just this aspect. I would not claim that you are wrong, but simply that you perhaps a bit overestimate the excitement you want the readers to show for your discussed observation. 
    Ladislav Kocbach | 01/06/11 | 05:29 AM
    Vladimir Kalitvianski
    Finally I found my error and I invite readers to see my pdf-file with detailed explanation. My problems were in making the preliminary calculations only in my head where I admitted a conceptual error and in sharing the unusual results without careful verification. Sorry!

    My statements are still valid for the expectation values, though.
    Vladimir Kalitv... | 01/29/11 | 05:15 AM
    Yes, but you can still set R=0 (after all, it is a change of reference system) and go across the painful process of quantising a system with a classical ligature or restriction. Dirac lectures on quantum theory focus in this paper, and at the end you should be able to relate partial angular momentum and total, see the consistency (or not) witth Clebs-Gordon coefficients, etc.

    Alejandro (not verified) | 01/07/11 | 02:14 AM
    Vladimir Kalitvianski
    No, the condition R = 0 is not a reference fame choice in QM but
    an unjustified constraint to the system motion. Normally the particles in a
    bound system are in mixed states, unlike quasi-particles. In particular, their angular momenta z-projections are never certain. Using the condition R = 0 may be tempting but wrong. That was my unforgivable mistake. So my statements are, in fact, applicable only to the expectation values of "personal" particle orbital momenta <n,l,m| l1,2 |n,l,m> since th expectation value of the fluctuating part Rx(d/dr) vanishes.
    Vladimir Kalitv... | 01/31/11 | 10:09 AM
    I think to remember that nuclear physicists (from whom you were part, time ago?) have developed some methodology to cope with the "center of mass correction" in the many body case.

    alejandro (not verified) | 01/07/11 | 05:42 AM
    Vladimir Kalitvianski
    If you speak of a nucleus as protons and neutrons, I did not participate in such activities. I worked with atoms and found it important to distinguish the center of mass variable R from the nucleus coordinate rN to correctly describe physics of scattering from atoms (http://arxiv.org/abs/0806.2635).
    Vladimir Kalitv... | 01/07/11 | 06:24 AM
    Ladislav Kocbach
    Dear Vladimir,
    I think this is all together extremely nice! I hope that you will let this post stand with pride! Here we shall have an example of a published "error" with various discussions. We all make errors all the time, but we correct them and forget about them (mostly). This could be a nice example of the strength of science 2.0 over the science 1.x.

    Thank you very much for all this!
    Ladislav Kocbach | 01/07/11 | 04:37 AM
    Vladimir Kalitvianski
    Yes, Ladislav, a feedback is very important.
    Vladimir Kalitv... | 01/07/11 | 05:15 AM
    have you heard feasibility of Bohr orbit quantization for multi-electron

    Anonymous (not verified) | 05/03/12 | 12:45 PM