A question posed by Tony Smith in the thread of the previous post (which dealt with the choice of the bin width in histograms) triggered me to do a little work to produce a convincing answer to him.

The issue is the following. Tony got interested in a few top candidate events in a few mass distributions published by CDF and DZERO quite some time ago, which seemed to all cluster in the surroundings of 145 GeV. Could those eight candidate events (once summed across the various channels and experiments) be the signal of some resonance different from top quarks ?

There are various ways to address this question. A simple one is to show that, once estimated backgrounds are subtracted, those eight events are compatible with anything -i.e., they are not demonstrable to be a signal of a new particle. But another way is to explain that the resolution in the top mass (or any other similarly decaying object) at 145 GeV is of the order of 20 GeV, so it is hard for eight events to cluster all in a 10-GeV-wide bin (between 140 and 150 GeV).

How hard ? That is the question Tony asked. Well, it takes very few lines of code to produce a meaningful answer, so here it is, in the graph below.

 The x axis in the figure shows the width of the hypothetical signal at 145 GeV, in GeV. The y axis is a probability. The black curve shows the integral of a Gaussian centered at 145 GeV in the range [140 GeV:150 GeV], as a function of the sigma one assumes for the Gaussian. As you see, the area in the interesting bin amounts to several decimals even for widths of 20 GeV.



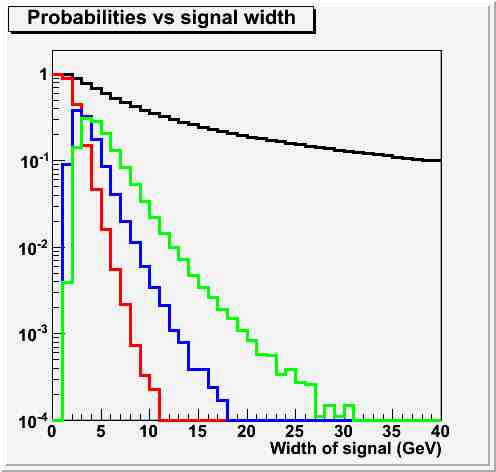
But then, ask yourself the question: what is the probability that with such a Gaussian signal, all of your eight signal candidate events fall in the 140:150 GeV interval ? You can see that described by the red curve. The probability drops to zero very quickly, because at least one or few events will "want" to spill out of the 10-GeV bin if the Gaussian sigma is not very narrow. The blue curve shows the probability that 7 out of 8 events are in the bin; the green one the probability that 6 out of 8 are.

In summary, we learn something: even small signals will hardly do you the favor of concentrating in one single bin, if your resolution is not much smaller than the bin width. But, as we have discussed in the former post, it is advisable to not make your bins wide.