And, update: rather than putting it at the end, I prefer to link Resonaances' post on the same subject here this time - he wrote about the matter yesterday and did a much better job than I do below. Sorry for noticing it after posting mine!
Some pedestrian kinematics
LHCb is one of the four detectors you may run into these days, if you are a 3.5 TeV proton. Less known than its bigger brothers ATLAS and CMS, LHCb still looks at the 7-TeV collisions delivered by LHC, but does so "sideways": only particles produced in and around the direction of one of the two beams are studied. The figure below shows a side view of LHCb, with a graph to decode the various pieces.
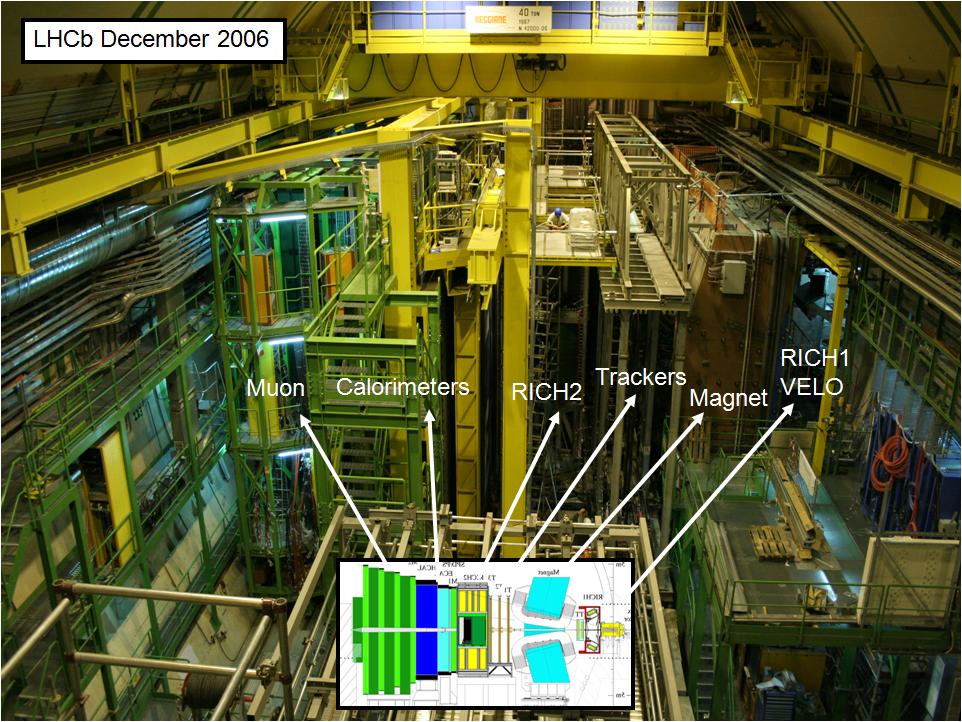
When a proton moving at an energy E1=3.5 TeV hits another proton moving in the opposite direction at E2=3.5 TeV, the nominal "center-of-mass" energy is E=7 TeV: E1+E2=E, simple math. However, this is a simplified picture, since the proton is not a pointlike object, and what we are in fact observing is the hard collision of a quark or a gluon in a proton with another quark or gluon in the other proton.
The center-of-mass energy of the hard pointlike collision is much lower than 7 TeV, and it depends on what fraction of the parent protons did the colliding constituents carry. If we take these fractions to be x1 and x2 (0<x1,x2<1), the effective collision energy in the two partons center of mass frame is 7 TeV multiplied by sqrt(x1*x2).
Typical values of x1 and x2 range from a thousandth to some tenths: the highest collisions we observe at the LHC have therefore an effective energy of two or three TeV at most. The relative probability of softer or harder collisions is governed by the parton distribution functions (shown on the left): these are probability density functions dictating how likely it is that a parton of a given kind is found with a fraction x of the proton's momentum. These functions are high at low values of x, so very energetic collisions are quite rare. But they do occur.
Now, to understand why physicists constructed colliding beam machines, you need to compare the center-of-mass energy of those head-on collisions with the one resulting when a single beam hits a fixed target. In the latter case, let us consider a 3.5 TeV proton hitting a proton at rest in the laboratory. The center-of-mass energy of the resulting collision can be calculated as the square root of the so-called "Mandelstam variable" s, working in four dimensions. It is actually much easier than you think. The math is the following:

In the first row we just expressed the fact that we are interested in the squared sum of the two incoming particles' four-momenta p1, p2. In the second row we explicitate this by separating the zeroth component of the four-vectors, E1+E2, from the three-vector of four-momenta; the minus sign comes from the "metric" of four-dimensional space-time. In the third row we substitute E1->E (incoming proton) and E2->M (proton at rest in the target, of mass M and zero momentum); we also take the z axis as the one along which the beam incides on the target. In the fourth row we just expand the squared parentheses, remembering that the first proton has momentum equal to E (it is ultra-relativistic) and the second has zero momentum. The result is that the center-of-mass energy in a fixed-target collision is sqrt(2ME).
So what would be the energy of a fixed-target collision of 3.5 TeV protons with still protons ? It would be equal to sqrt(2ME)=sqrt(2*1 GeV * 3500 GeV) = 85 GeV: quite small! We would be kinematically prevented from even producing a Z boson with such arrangement... And note that we have not even factored in the two partons fractionary momenta x1 and x2 in the calculation above. The smallness of the available energy to produce new heavy particles in fixed-target collisions is the reason of constructing particle colliders.
Back to LHCb
But LHCb, as I stated above, only looks at one of the two sides of the collision: it basically observes collisions which have one of the two partons much more energetic than the other. If x1>>x2, we are tantalizingly close to the kinematic regime of fixed-target collisions: the total center-of-mass energy is much smaller than the one available to central collisions, where the two partons carry similar fractions of their parents' momenta. Of course, LHCb also "sees" the one-sided view of central collisions, by intercepting the remnants of one of the two proton and the resulting fragments; but similar kinematical observations apply: the reaction energy available in the forward region is small.
You might thus think the whole concept is a weird idea: we have spent decades trying to move away from the fixed-target arrangement and into the colliding beams configuration, making our beams more dense and intense in order to produce sufficiently high collision rates (something that fixed-target arrangements provided from day one) in order to reach higher in center-of-mass energy, and now we use these lower-rate collisions to study a lower energy regime ?
Well, it is not so weird. The fact is that a 3.5 TeV proton beam can only be produced at the LHC these days. And the resulting "lower-energy" collisions are in fact very interesting: they produce huge amounts of fast-moving heavy quarks, something that lower-energy fixed-target collisions did not do. The resulting B and D hadrons (ones containing bottom and charm, respectively) are invaluable to measure precisely some parameters of the standard model which CMS and ATLAS are less suited to study.
One additional bit of information
The measurement of direct CP violation in D mesons is one of these pieces of physics which LHCb is best suited to perform. The advantage of the LHCb arrangement with respect to ATLAS and CMS is that the hadrons it observes are very energetic, and thus travel long paths before decaying. Here I need to explain another bit of kinematics.
When a particle with a lifetime t is at rest, there is a probability 1-1/e=63% that it decays in the next t seconds: this is governed by the well-known exponential decay rule. But when we see the particle moving, Einstein taught us that there is a mismatch between the time as measured in its rest frame and the time as we measure it. This mismatch is proportional to the "gamma factor" of its speed. Without going into formulas, we can get away by saying that for a particle of energy E much larger than its rest mass M, gamma=E/M is large. The 63% probability that it decays occurs now at a time t'=gamma t.
What the above tells us is that we may see a 100-GeV charmed meson D, for which t is a few tenths of a picosecond, decaying in a time t'=50 T, since gamma is about 50 for it (its mass is M=2 GeV). Experimentally, this factor of 50 is quite important, since rather than traveling, say, 500 micrometers in the detector before disintegrating, the D meson travels one inch! We can thus "see" much more clearly its decay vertex and distinguish it from the point where it was created, rejecting backgrounds more effectively and making all of our measurements much more precise.
In CMS and ATLAS, 100-GeV D mesons are rare, since those 100 GeV must originate from the released energy of the collision. In LHCb, instead, those 100 GeV are not so rare, since we are observing the particle moving in the same direction of the original proton: for the same reason if you are standing near somebody who is being thrown a pie, you move sideways, not behind him - remnants of the pie will be much less likely to reach you then.
The measurement
So it is LHCb the first experiment which measures a direct CP violation effect in the charmed meson system. The measurement we are discussing is a "3.5-sigma" one, so we are talking about a "first evidence" of a CP asymmetry: there is still a small, but not totally negligible, chance that the measurement of a non-zero asymmetry is due to a fluctuation. Before we go to a graphical illustration of the result, let us see how it came about.
A CP asymmetry results if a particle and its antiparticle behave differently. This is possible in the standard model, due to several small effects; it can be studied best in rare decays of heavy mesons, where the CP-violating effects are relatively larger. New physics could manifest in an enhancement (by some percent) of these asymmetries with respect to the standard model prediction, so their study is a way to probe the standard model in a way which is independent on the high-energy searches that ATLAS and CMS are doing.
LHCb tested the decay properties of neutral D mesons, particles composed of a charm quark and an anti-up quark, and anti-D mesons, which contain a up-quark and an anti-charm one. They did so in a sample of 580 inverse picobarns of proton-proton collisions collected this year (about half of their total dataset), by studying the rate of D meson decays into pairs of kaons (K+K-) or pions (pi+pi-). The identity of the D mesons (i.e., the presence of charm or anticharm in them) is first "tagged" by their production together with an additional soft pion in the decay of D* mesons (the charge of the pion discriminates the two), and then carefully studied to avoid or correct any detector-related effect which might pollute the measurement.
The quantity that LHCb extracts from the measurement is actually not a single CP asymmetry, but the difference of two separate ones: the one of the D decay into kaon pairs minus the one of the D decay into pion pairs. Many detector-related effects cancel in the difference, so the measured quantity is much more precisely determined; but further, the "indirect" component of the asymmetries cancel in the difference, leaving only the direct part. This is a technical point which I will leave unexplained, but just mention that indirect CP violation arises from the mixing of the D mesons, and from related interference effects.
In the end, a global fit of mass distributions as a function of the kinematics of the candidates allows to better gauge the residual detector effects. The result of LHCb is that the CP asymmetry equals -0.82+-0.21(stat)+-0.11(syst)%, a number which differs from zero by 3.5 standard deviations. The graph below illustrates what is measured in the plane spanned by direct (in the vertical axis) versus indirect (horizontal axis) asymmetry: the LHCb band is almost horizontal, indicating that the measured asymmetry is largely coming from direct CP violating sources.
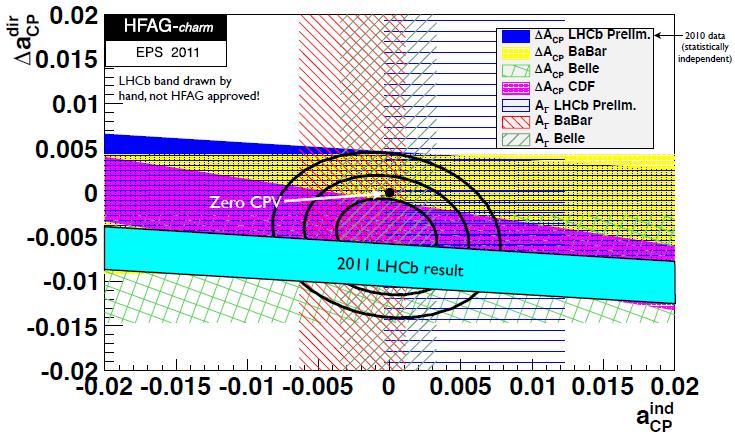
The result is compatible with the previous measurements by other experiments, but it is the first one which deviates significantly from zero, as is visually evident by looking at the "distance" of the black point from the cyan band. The black ellipses show the previous world average for the CP violating asymmetries, while the different bands illustrate the results of previous experiments, formerly dominated by the CDF result.
LHCb will be able to improve the statistical accuracy of this result in the near future, by doubling the analyzed dataset. One might naively expect that their total uncertainty might shrink to sqrt(0.5*0.21^2+0.11^2)=0.18, which would produce, in case the central value did not move around much, a result differing from zero by over five standard deviations. Time will tell! In the meantime, I congratulate with the LHCb colleagues for this very careful and difficult analysis.



Comments