I have recently dusted off an algorithm I had invented eight years ago, one I dubbed "Hyperball algorithm". It might come handy for predicting the b-tagging rate in CMS events with jets, for an analysis I am thinking of doing. Since saying more would violate a dozen rules so let's leave it at that, and let me instead describe the old idea... Just for fun.

Predictions for the Higgs at the Tevatron

Eight years ago the Tevatron was the only player of the Higgs hunting game. LEP II had just left the scene with its 1.7 sigma indication that something might be cooking at a tentative mass of about 115 GeV, and the CDF and DZERO experiments were trying to make the case for further upgrades to the detecting elements, with the Standard Model Higgs boson set as the ultimate prize.

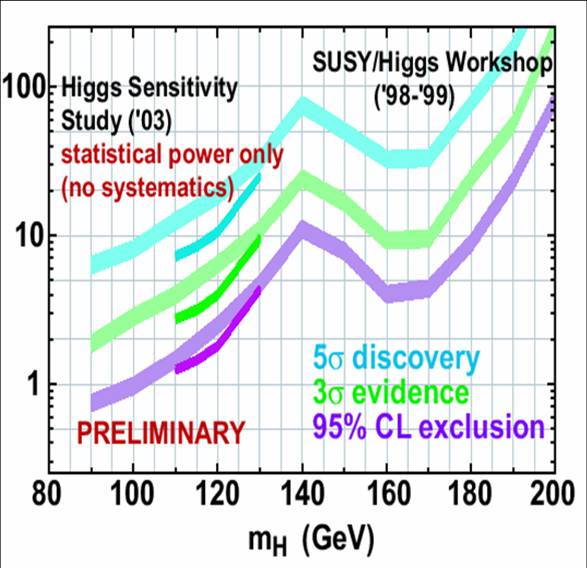Four years earlier (in 1999 to be exact) the Tevatron SUSY/Higgs working group had already assessed the chances of a Higgs boson discovery or exclusion by the CDF and DZERO experiments (see figure on the right), but by 2003 there was real data to play with. This made all the difference: while the 1999 study had been based on a simplified simulation of the "average" detector to evaluate the sensitivity to the Higgs boson as a function of the particle's unknown mass, now real data could be used to precisely assess the background levels of every specific search, the lepton-finding efficiency of the two detectors, and their b-tagging capability.

The standard ingredients

Perhaps I should explain what all these things mean. First of all, the Higgs boson is produced, if it exists, quite rarely in the proton-antiproton collisions delivered at 2 TeV energy by the Tevatron collider. And the rarity of its production is a function of its mass: the higher the mass, the fewer events are expected in a given dataset. This is the result of the increasing rarity of quarks and gluons as the fraction of the total proton momentum they carry is increased: the hard collision takes place between quarks and gluons, and it takes more energy to produce a more massive Higgs boson.

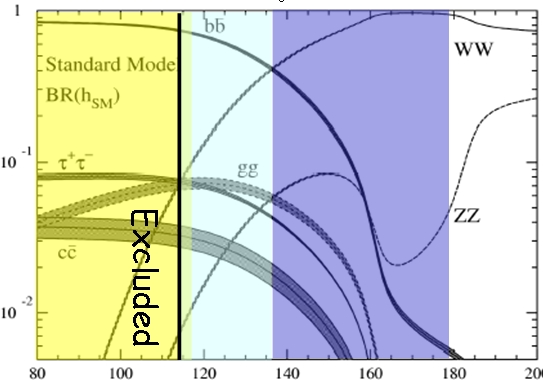But the mass also determines into what bodies will the Higgs boson decay: if the mass is lower than 135 GeV or so (pale blue region on the left), the decay into a pair of bottom quarks dominates, while if the mass is higher (purple region) the decay into W boson pairs is the most frequent one. Not knowing the mass, one must take that as a parameter, and study the signal detection capabilities for different masses. The figure above describes the possible ways a Higgs boson disintegrates, with their relative frequency plotted as a function of the unknown mass. As you can see by yourself, at low mass the H-->bb decay is the most frequent one, topping at about 90%. For masses close to 160 GeV, on the other hand, the H->WW decay is totally the most likely one. (The figure also shows the region already excluded by LEP II, in yellow. This is an old figure -a newer version would have a similar yellow band spanning the region 158-173 GeV, as the Tevatron has recently excluded that portion of the mass spectrum).

At low mass both the efficiency to detect electrons and muons and the efficiency to identify bottom-quark jets count, because the Higgs is sought in events where it is produced together with a W boson, and the W boson decays into electrons or muons; then, in order to reconstruct the H->bb decay, the two b-quarks must be distinguished from backgrounds, so b-tagging becomes essential. In contrast, searching for Higgs bosons produced alone is hopeless, since the H->bb decay is totally swamped by direct production of two b-quarks by quantum chromodynamical processes which have a total rate a million times larger.

At higher masses, on the contrary, the Higgs can be studied as well when it is produced alone (i.e. not accompanied by a W boson) because the decay into a pair of W bosons is distinctive enough to grant a simple collecting at trigger level. All in all, we can summarize the above by saying that the most important ingredients for the Higgs search are leptons and b-quarks.

Projections of sensitivity

Okay, now that I have explained that detail, let me get back to the reason for the 2003 study. The Tevatron experiments were already running at a steady pace by then. An upgrade of their silicon systems (the ones responsible for the b-tagging capabilities of the detectors) was thought important to increase the acceptance to b-quark jets, as well as to guarantee that the aging to which silicon sensors are subjected because of their high doses of radiation would be addressed by replacing the inner layers. The 1999 study had shown that there was hope to obtain a first evidence of the Higgs at low mass, so the matter had to be studied in more detail with the increased knowledge of the detectors and the backgrounds.

I took part in the 2003 group which reassessed the Higgs discovery chances of the Tevatron experiments. This was called "Higgs Sensitivity Working Group" and it was a serious business: we were supposed to not just turn a crank, but to come up with smart ideas on how to increase the sensitivity of the experiments. This meant, among other things, to focus on the critical aspects of the Higgs search and improve the search strategies.

Besides lepton acceptance and b-quark tagging, there is a third, crucial aspect of low-mass Higgs searches at the Tevatron. This is the mass resolution of pairs of b-quark jets. If one had a perfect detector, which measured very precisely the energy possessed by b-quarks emitted in the Higgs decay, it would be relatively easy to discern even a small signal: the invariant mass of signal events would always be the same, e.g. 120 GeV, while backgrounds would distribute with a flat shape, so that the signal would appear as a narrow bump on top of the flat background.

Alas, jets are complicated objects, so the mass resolution of pairs of jets is affected by many problems that reduce it. A narrow spike then degrades into a Gauss-shaped hump, which easily get washed out on high backgrounds if the width of the Gaussian is not kept as small as possible. This requires one to employ advanced techniques to try and infer with all the possible observed quantities in the detector whether a jet was measured lower than the true originating parton, or higher, and correct for the effects that caused the bias.

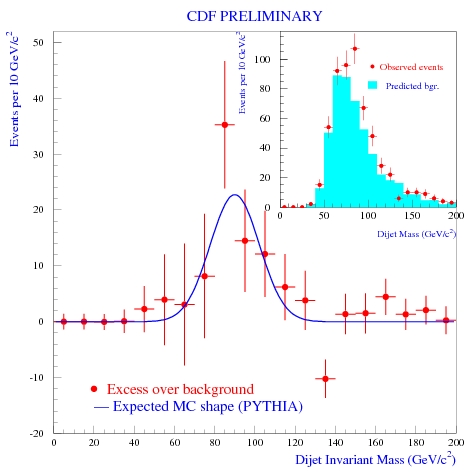I had worked on the reconstruction of the Z->bb decay signal in CDF data for my PhD thesis (see my original plot on the right: the inset on the upper right shows the data (red points) and the background prediction (blue histogram); the larger plot shows the excess, with a Gaussian fit overlaid), and so I was rather expert on these issues. I therefore set out with enthusiasm to find a way to improve the dijet mass resolution for pairs of b-quark jets produced by Higgs decays.

I soon became convinced that there are many possible measured quantities in our detectors that contain information on whether a jet's energy was under- or overestimated. Too many, actually, to enable a meaningful, systematic study. The particle content of the jet, their spread around the jet axis, the distribution of momenta of charged tracks, the characteristics of the b-tagging vertex they contain; but also other quantities measured in the event, like the missing transverse energy, the angles between jets and lepton. A truly multi-dimensional problem!

20 dimensions - or maybe 40

I decided that the problem was one of simply computing an "average bias" in the mass measurement of a pair of jets. This bias would depend on the dozens of observable quantities that might affect it in hard-to-tell ways. With a Monte Carlo simulation, one could estimate the bias depending on the value of these observable quantities, and correct for it. But how to compute a meaningful "average" in this multi-dimensional space ?

The problem was that if one has D=20 (or even more) space dimensions, each representing a different observed quantity along with the ones used to reconstruct the dijet mass, any Monte Carlo simulation will run out of statistics before one can meaningfully populate the possible different "bins" of this multi-dimensional space. That is, let us assume that one divides each of the 20 variables into three bins: low, medium, and high values of each. This creates 3^D=3 billion bins (for D=20). Even if one had a huge simulation with a billion Higgs boson decays, the bins would never contain a meaningful number of events with which to compute an average bias (e.g. true Higgs mass minus measured mass).

There was a way out. One needed to stop thinking in terms of a discrete matrix (as was the typical approach), but in terms of continuous variables. I wrote an algorithm that did precisely that: if you had a real data event with a measured mass M and with a certain value of the 20 variables, you could move around in the neighborhood of the point in the 20-dimensional space corresponding to the data event, and ask to each Monte Carlo event lying nearby in the space whether the reconstructed mass one could compute with it was over- or undermeasured. If one asked enough events for a meaningful average, that would be enough!

So one needed to "inflate" a hyperball in the multi-dimensional space, capturing Monte Carlo events that were "close enough" to the data event to be corrected. One needed to define properly what it meant to be "close", in a space defined by space coordinates which had different measuring units and ranges, but that was the easy part. The hard part would be to find the proper shape of the hyperellipsoid within which to compute the average bias in the mass measurement.

In the end, the algorithm proved to work wonders, increasing the mass resolution by 30%. This, together with other improvements of the analyses, allowed the Higgs sensitivity working group to assess the Tevatron chances rather favourably in teh low-mass region. I wrote about the algorithm in a post a long time ago, see here for some more detailed explanations...

Anyway, in the end the main result of the HSWG was to confirm the old predictions (which were thought to be highly optimistic back then). You can see that in the first figure above, where the 2003 results are shown overlaid to the 1999 ones. Note that the HSW group worked under the hypothesis that an upgrade of the silicon detectors would be installed: the later results of Higgs searches at the Tevatron have underperformed in the low-mass region, but at least part of this is due to the absence of the funds necessary for a cool retrofit of the silicon detectors.

By the way, you can find much more information on the above issue, on the underperformance of the Tevatron at low mass, and of various opinions on the matter in a post I wrote to comment an obnoxious seminar by Michael Dittmar a couple of years ago.

So, all in all this long post is just to say that I have resurrected the old algorithm, which was never used in a real physics analysis. I want to use it this time! I am sure it is very powerful, and although it has some CPU issues (the time needed to sort out the closest events in a large-dimensional space), I am sure it can produce results at least on par with other multi-variable tools. Time will tell...