The measurement of the production cross section of this clean and rare electroweak process (its absolute rate, that is) is the most precise ever obtained so far, and reaches down to a level of uncertainty which cannot be improved further significantly at the Tevatron, because it is now limited by the uncertainty in the overall integrated luminosity mentioned above.
For me, it is literally a joy to see such a wonderfully accurate measurement coming out, for a process which was only seen with difficulty twelve years ago: we used to know the few events one by one back then, but now there is a 600-event sample of diboson candidates isolated by CDF, which contains over 300 genuine WW events. Besides a careful determination of the cross section, the sample is the starting point for Higgs boson searches, as well as to test several new physics scenarios.
Higgs bosons become a relevant source of diboson events if the Higgs mass is higher than about 135 GeV, which makes the H->WW decay the most probable. Regardless of the Higgs mass, however, the ratio between the two sources of dibosons -general electroweak quark-annihilation diagrams, and production from H decay- is very large at the Tevatron: the standard model (SM) process is over one order of magnitude more frequent. So, unless one explicitly attempts to look for the corners of phase space where H->WW is favoured, one may simply neglect that "contamination" of the diboson sample.
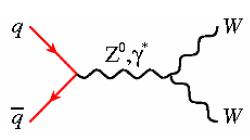
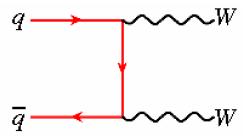Much more interesting is the fact that through WW events we gain access to a direct measurement of the triple-gauge-boson coupling (TGC), a quantity which determines how likely it is that an electroweak vector boson (a W, or a Z, or a photon) emits another one. There exist different configurations of possible boson emissions: the one relevant to WW production is the one which occurs through the production of a virtual Z or photon, shown in the diagram on the left. The diagram on the right, instead, is still a SM process but it is not sensitive to the value of TGCs. The two processes are not measured individually, but a grip on TGCs can be obtained from the total rate.It so happens that triple gauge boson couplings are very-well predicted in the Standard Model -their value boils down to very well-defined expressions in the electroweak lagrangian density function. As you may guess, from the value of a few basic constants in the Lagrangian, it is possible to compute a very definite value of the cross section of processes involving three bosons joining at a vertex. It is not as simple as calculating a mortgage installment from the interest rate, but not intrinsically different either.
Now, here comes the neat part: there are models of new physics that would modify those TGCs in a quite striking way, providing new observable features in diboson events. In particular, the excess events caused by increased, anomalous couplings would not just cause a higher production rate, but concentrate the enhancement at high values of transverse momentum of the produced bosons. By studying the transverse momentum distribution of electrons or muons produced in the decay of the W bosons, a powerful test is possible for these anomalous TGCs.
The CDF measurement
Events are selected with the requirement that they feature two high-transverse-momentum leptons (electrons or muons), plus a large unbalancing of the energy in the transverse plane, the so-called missing transverse energy. The missing transverse energy is a signature of the production of neutrinos, a pair of which must accompany the two charged leptons in the decay
I wish to note that for once I have been accurate in the notation of the decay chain above: the "X" is needed to summarize the fact that the WW pair is sought inclusively, whatever else is produced together with it. However, this should not be taken to mean that the process ttbar ->WbWb is considered as part of the signal: these events are almost totally removed from the sample by the application of a tight jet veto targeted at the two b-quark jets which top pair decays always produce. The "X" just labels additional hadronic activity in the production of W boson pairs.
The measurement performed by CDF relies on a matrix-element calculation of the probability that events belong to each of the possible contributing processes. I will not bother you with explaining how those probabilities are actually computed, but maybe an example can give you some idea.
Suppose you share an apartment with Joe and Mark. One night you come home late and need to talk to Mark; there is one person in the bedroom, and there are remains of a dinner on the table. You do not want to wake up Joe by mistake so you do not go in the bedroom straight away: you have several data to work on in order to guess whether it is Joe or Mark who dined there and then went to bed. Joe is less likely than Mark to drink beer, but if he does he drinks more than Mark; Mark tends to avoid meat; and so on. From the precise knowledge of the eating habits of your colleagues you can construct two global probability estimates of having observed two empty beer bottles, remains of meat, etcetera: we like to call these P(dinner table|Joe) (read it "probability to observe the remains on the table given Joe dined there") and P(dinner table|Mark).
The matrix element method similarly extracts P(kinematics|WW), P(kinematics|Z), and so on, from the observed quadrimomenta of leptons, jets, and missing energy. These probabilities are then used to compute a likelihood ratio estimator. This function discriminates genuine WW production from all backgrounds, which mainly belong to three classes: single W bosons produced together with a jet, Z bosons, and W bosons produced together with an energetic photon.
In the first case, the jet may fake a second electron or muon, but its rate can be reduced by tight identification and isolation requirements on the leptons; in the second case, the two leptons from Z decay may fake a WW event if the additional hadronic activity is mis-measured, causing missing transverse energy; in the third case, the additional photon may be reconstructed as an electron candidate, producing the required dilepton signature.
The definition of the likelihood ratio is straightforward. You take the probability that the event is signal, and divide it by the sum of all probabilities:
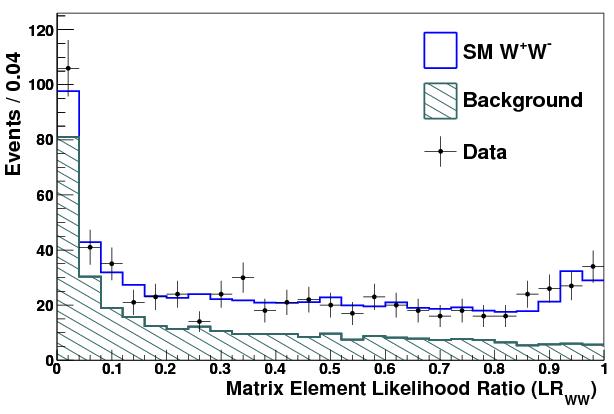
Below you can see how the data distributes as a function of the likelihood ratio: high values of course correspond to the most signal-like events. The empty histogram represents the signal, the hatched one is the background contribution.
Sensitivity to anomalous TGCs is then obtained by displaying the two components of the data as a function of the transverse momentum of the stiffest lepton. In the figure below you notice that if anomalous couplings are assumed (dashed lines with different colours, corresponding to different values of the anomalous coupling), the spectrum becomes considerably more populated at high values of the plotted variable. What is suggestive, however, is that the data does seem to prefer a enhancement at high momentum with respect to the standard mode prediction (blue histogram)!
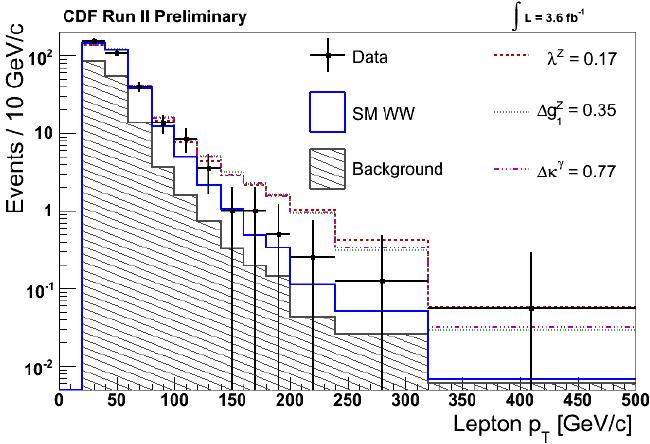
The high-Pt enhancement is objectively mild: the probability of overall agreement with vanilla Standard Model with no anomalous couplings is not too small -of the order of 7 percent or so. Still, in the process of setting limits to these anomalous couplings, CDF obtains a worse result than it would have if the data had lined up better with Standard Model predictions.
Maybe a telling figure is the one reported below, which shows on the vertical axis the likelihood of the transverse momentum distribution observed in the data as a function of the value of one of the three unknown anomalous coupling constants -which should be zero in the Standard Model.
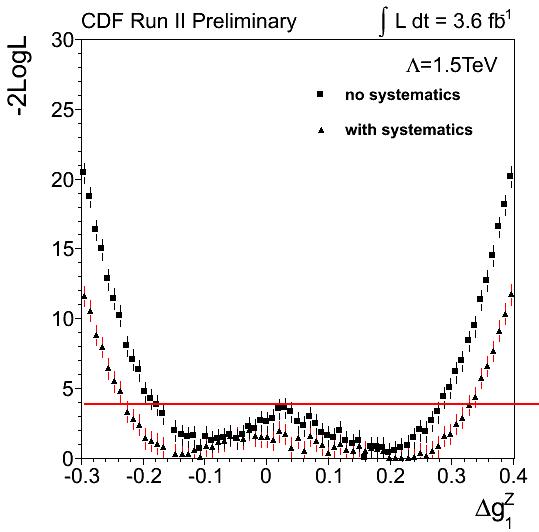
As you can see, the data do prefer, albeit not by much -one or two units of likelihood- a non-zero value of the coupling shown on the horizontal axis. The horizontal line at 4 determines the region which is allowed by the present data, on the parameter shown.
Conclusions
The production of pairs of W bosons has been studied by CDF with a large dataset, and the most accurate measurement of its cross section has been obtained: the cross section reads
The presence of more high-momentum leptons than expected in the sample suggests that the WW sample should be watched in the future: with larger statistics, the same discrepancy shown above might one day become a solid evidence for anomalous couplings!
Comments