Two things can happen: either all players are asked for the value of X, or one player is asked for the value of X while the two other players are asked for the value of Y. The possible values of X and Y are +1 and −1.
If all players are asked for the value of X, they win if (and only if) the product of their answers equals −1. If one player is asked for the value of X while the two other players are asked for the value of Y, they win if (and only if) the product of their answers equals +1.
Once the questions are asked, the players are not allowed to communicate with each other. Prior to that, they may work out a strategy. My question was: Is there a fail-safe strategy? Can the players make sure that they will win?
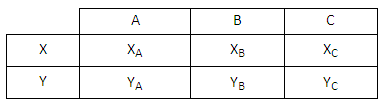
In other words, is it possible to assign values (+1 or −1) to the elements of this table in such a way that they satisfy all of the following equations?
XA XB XC = −1
XA YB YC = +1
YA XB YC = +1
YA YB XC = +1
As we figured out in the comments to my previous post, the answer is negative.
One way to quickly see this is to form the product of the left-hand sides of the last three equations: XA XB XC (YA)2 (XB)2 (YC)2 = XA XB XC (because all squares are equal to +1). Since the product of the right-hand sides equals +1, it follows that the first equation cannot hold if the last three do.
And yet there is a fail-safe strategy.
Quantum mechanics allows us to prepare three particles A, B, C in a specific manner and to subject each to either of two measurements X, Y, so that the outcome of each measurement is either +1 or −1, the product of the three outcomes is −1 if each particle is subjected to a measurement of X, and the product of the three outcomes is +1 if one particle is subjected to a measurement of X and the two other particles are subjected to a measurement of Y.
Thus if Andy, Bob, and Charles each take along one particle and perform the appropriate measurement, they are sure to win every time.
Next question: Can the outcomes obtained by these measurements reveal pre-existent values? For the same reason that pre-agreed answers cannot ensure a win, the answer is negative.
Technical interlude (may be skipped):
The three particle are spin-1/2 particles, and the state in question is
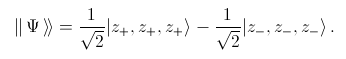
This can be cast into the following forms:
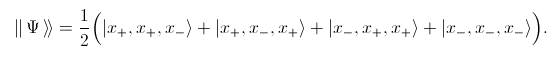
Note that each of the four terms contains an odd number of minus subscripts.
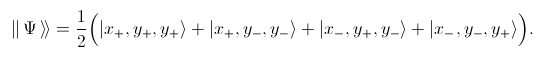
Here each term contains an even number of minus subscripts. Since the first equation is invariant under permutations of the three spins, we obtain another two equations with x in the second and third place, respectively.
References: "Going beyond Bell's theorem" by Greenberger, Horne, and Zeilinger, in Bell's Theorem, Quantum Theory, and Conception of the Universe, edited by M. Kafatos (Kluwer Academic, 1989), pp. 69−72. The game version of the GHZ experiment is due to Lev Vaidman ("Variations on the theme of the Greenberger-Horne-Zeilinger proof" in Foundations of Physics 29, 1999, pp. 615−630). The first experiment of this type was performed by Bouwmeester, Pan, Daniell, Weinfurter, and Zeilinger ("Observation of three-photon Greenberger-Horne-Zeilinger entanglement" in Physical Review Letters 82, 1999, pp. 1345−1349).
(End of technical interlude)
By the time GHZ published their paper, it was all but taken for granted that the contradictions between quantum mechanics and the assumption of pre-existent values ("elements of physical reality'', as Einstein used to call them) are essentially statistical, like the one discussed in my previous post. When GHZ showed, by using an entangled state of three particles, that pre-existent values can be disposed off through a single false prediction, it caused quite a stir.
To arrive at a false prediction, suppose that YA, YB, and YC have been measured. We could then reason as follows:
If XA had been measured instead of YA, the outcome would have been XA=YBYC.
If XB had been measured instead of YB, the outcome would have been XB=YAYC.
If XC had been measured instead of YC, the outcome would have been XC=YAYB.
Hence if XA, XB, and XC had been measured instead of YA, YB, and YC, the product of the outcomes would have been equal to (YA)2(YB)2(YC)2=1. Which of course is the wrong answer.
Since the above measurements do not reveal pre-existent values, we have to conclude that they create their outcomes. The only sufficient condition for the existence of a value is to be measured. The GHZ experiment amply justifies Bohr's insistence that, out of relation to experimental arrangements, the properties of quantum systems are undefined. Bohr, who like Einstein did not live to see even Bell's theorem of 1964, would have been as happy with the result of GHZ as Einstein would have been unhappy.
Observe that on the basis of any two outcomes, the third outcome can be predicted. If, for instance, we measure XA and XB, we can predict (correctly) the outcome of a measurement of XC.
Next question: How is this possible, considering that the relative timing of the three measurements is irrelevant, and that in principle the three particles can be miles apart? How do the first two measurements (or their outcomes) influence the outcome of the third measurement? What physical mechanism or natural process is at work?
You understand this as much as anybody else.




Comments