I found a better use of the stream. By standing in the 4' deep water with my back facing the water jet, I found I could let my body tilt against the stream, until the gravitational pull was in perfect equilibrium with the pressure from the stream. The position of perfect equilibrium, in fact, appeared to be rather forgiving -indicating that a small variation of the angle of my body did not change much the situation. In the meantime, the water massaged my back quite pleasantly. Finally a way to put to work the physics I studied hard in high school!
Back in my hotel room, I reasoned that the problem is actually fun to try and schematize. There are several ingredients, which make it less than trivial; actually, if one wants to solve it reasonably one needs to apply quite a few approximations. There are several forces at work: the gravitational downward pull on the body; the reaction of the point of contact with the bottom floor of the pool; the upward pull of the mass of water displaced by the body; and the pressure on the body caused by the water jet, for which one must hypothesize some functional dependence on the distance from the source -I suspect the real formula is not at all simple.
From a qualitative standpoint things are easy to figure out: the body wants to fall backwards as it is tilted from the vertical; but the effective gravitational pull is not stronger as the tilt angle increases, because as the body sinks further in the water the effective weight decreases (until it zeroes if we assume that the body has the density of water). In the meantime, a larger tilt brings the back closer to the stream, so the pressure increases. The result is a shallow equilibrioum region, for a wide variety of configurations (I tried a few).
And now quantitatively: let us take a two-dimensional approximation; the body can be approximated by a bar of l=1.8 meters length, with a weight m=75 kg, and the density of water (such that if fully immersed the gravitational downward pull equates the upward pull from water displacement). The water stream can be approximately estimated to provide a force, integrated over the area where it invests the body, of F=50 Newtons at one meter distance, with a 1/x dependence on distance (other hypotheses can be tried, but I suspect this is not the critical part of the problem). The jet of water is taken to come from a height of h=1m from the bottom of the pool, and H=1.3 m. Let us also take D=1.8m.
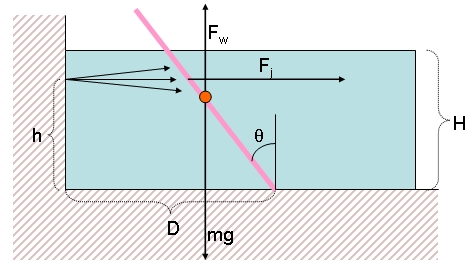 A sketch may help us out. On the right you see the body in the water schematized as a pink rod. Its center of mass is taken at its center (a rather sloppy approximation, but let us not be too picky), and it is labeled by a orange circle. Two forces act on the body's center of mass: the downward gravity pull mg, and the upward push which depends on the amount of water displaced, Fw. A third force Fj is caused by the water jet.
A sketch may help us out. On the right you see the body in the water schematized as a pink rod. Its center of mass is taken at its center (a rather sloppy approximation, but let us not be too picky), and it is labeled by a orange circle. Two forces act on the body's center of mass: the downward gravity pull mg, and the upward push which depends on the amount of water displaced, Fw. A third force Fj is caused by the water jet.You may have noticed that I ignored any reaction in the point where the body stands, at the bottom of the pool. We may ignore these forces because we are going to take that point as the center of rotations: all forces passing through it have a null effect on the rotation of the body.
The problem thus reduces to determining the angle theta for which the three forces exert zero total momentum of rotation. These momenta are: M1=-mg l/2 sin(theta), M2=mg l/2 sin(theta) * H/(l cos(theta)), and M3=Fh/(D-h sin(theta)). Finding the angle theta for which these three momenta zero out solves the problem. Want to try it ? I am too lazy, but you might find it fun... Let me know what you come up with!
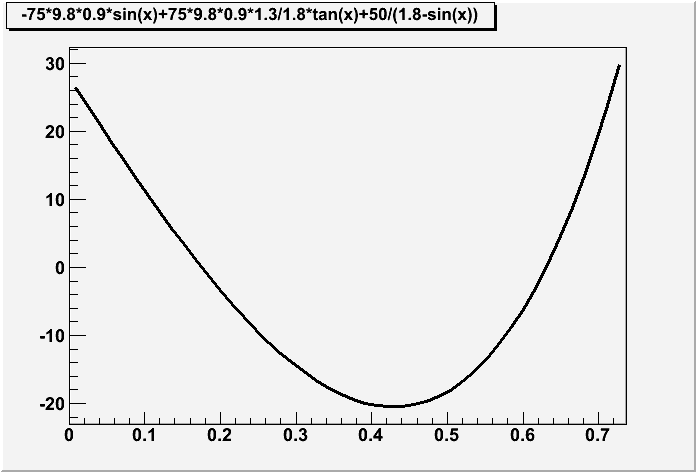
UPDATE: Note that a force F=100 Newtons at 1 meter distance is too strong for the water jet, and no equilibrium can be found in that case. This I could only find out after trying to solve the problem myself... Apologies to whomever tried to solve the problem numerically already. A force F=50 Newtons at 1 meter (and a 1/x dependence on distance, as stated above) is more appropriate. With it, I find two equilibrium points at about 10° and 36°. A torque pushing the body towards smaller angles is exerted between these values, and an opposite torque acts outside that range. The result is that small oscillations can be established around the equilibrium points. The torque is shown in the graph below (units on the x-axis, representing the angle theta, are radians):




Comments