The reading of the paper titled "Triple-Top Signal of New Physics at the LHC" gave an answer to quite a few questions I had been asking myself. What is the rate of production of three or more top quarks in the proton-proton collisions that the Large Hadron Collider at CERN will start producing at the unprecedented energy of 7, 10, and ultimately 14 TeV in the next few years ? Will we be able to pinpoint those very peculiar processes ? Will their study shed light on anomalies in the Standard Model of particle physics, ultimately leading us to the discovery of new physics ?
Some background on top quarks
In order to let you figure out what the heck I am talking about, I need to explain some very basic facts about the production of rare processes in proton-proton collisions. First of all, let me introduce you to the top quark, the heaviest elementary body we have ever discovered this far.
The top quark is a very peculiar subatomic particle: it is virtually point-like as far as we can tell with the microscopes we have at our disposal (the highest energy particle accelerators), but still it weighs just a tad less than a whole gold atom (or, if that surprises you more, just about as much as ten molecules of water!). This concept, by itself, is already confusing, until we accept that "mass" at the quantum level is not the same thing we experience in our everyday life.
Still more strange is the fact that the top quark lives on average less than a trillionth of a trillionth of a second: a time so short it defies even the steepest comparison with things we have experience with. Top quarks decay so quickly after they are produced in a energetic collision, that they are not affected by the strong charge they carry, which would bind them inside hadrons if they lived longer: gluons -the jail guards of quarks- do not even have the time to realize a top quark has evaded their surveillance.
Top quarks make very interesting study ground, because of the above properties as well as others that I cannot fully explain here. But most importantly, their production is very rare if catalyzed by known Standard Model processes. This is an appealing property!
Smallness is an asset
Experimental particle physicists love to study processes which are predicted to be rare just as much as they like to measure things that are predicted to be small, because both their rarity or smallness makes them sensitive probes. To explain this, imagine you need to test a theory which says that an angel rests on the shoulder of every living creature on earth every December 25th. Angels must be pretty light: from previous experiments and other deductions you know that if they exist they weight less than a gram. You would love to determine their weight, and especially to measure it to be significantly different than zero. That would be a tentative discovery of angels! It would not prove that angels exist, of course, since other causes may have produced the observed weight gain; but the angel theory would certainly start to be considered more seriously, and you would get lots of quotations from the Vatican press.
You might detect the change of weight due to an angel with a very precise scale by recording the weight of a living creature on December 24th and 25th, then comparing the two measurements. Would you pick an elephant or an ant to perform the angel-weighting experiment ? They are both living creatures and so theory wants them both to carry an angel on December 25th, but of course the ant would be more appropriate, because you would much sooner detect a variation of one gram in its weight, rather than on the weight of the elephant!
The stupid example above describes two essential facts about the search for rare phenomena. The first is that you want to detect a tiny variation in some physical property, so your testing ground is one where tiny things stick out! If new physics manifests itself as a very small increase in the production rate of some subnuclear process, the background -that is, the known part of the phenomenon, like the weight of the living creature- needs to be as rare, or small, as possible. The second fact is that a new theory is not proven to be correct by a positive confirmation: a theory is a theory, and it remains such even after colossal amounts of proof! Such is the destiny of the Standard Model, as much as that of any other construct we have put together to explain the features the world around us.
Top production in some detail
So what are the processes that produce top quarks in high-energy proton-proton collisions at the Large Hadron Collider ? There are very many, but they can be fruitfully divided in two classes: ones due to the intervention of the strong interactions, and ones due to the intervention of electroweak interactions. Below I will provide them as building blocks before we construct a full subatomic process capable of producing three top quarks together.
1 - a gluon (a particle of zero mass, carrying the strong force) may split into a top-antitop pair. In order to do that, the gluon must be extremely energetic: it must carry an energy equivalent to at least twice the mass of the top quark. We say that the gluon has a very high "virtuality": unlike normal gluons, which have close to zero energy, this one must carry at least 350 GeV. Beware, this is not the energy of the gluon in a proper sense: it is its mass -highly virtual, because largely different from its usual value, zero.
I have to also say that the gluon does not like much to split into a top-antitop pair: given a choice, a gluon would sooner produce a gluon pair rather than a pair of top quarks (other lighter quarks are also possible, but then the gluon is democratic in its choice of quarks). The real reason for a suppression of top pairs as a final state of the splitting of a 350 GeV gluon is however that in order to split to two tops the gluon needs to administer to each precisely the correct amount of energy needed to form their rest mass (172 GeV), and then very little energy is left to provide the two daughters with cruising speed. This is what physicists call "phase space suppression": I have discussed it in some detail in a recent post. Note that we might well imagine that the gluon had 1000 GeV of virtual mass, and in that case the phase space suppression would be close to irrelevant: but a 1000 GeV gluon is enormously more rare than a 350 GeV one!
2a - a Z boson (the neutral electroweak particle discovered by Rubbia in 1983, a particle with a nominal mass of 91 GeV) may also split in a pair of top quarks. In order to do that, the Z must also have a mass in excess of twice the top quark mass, so it has to be highly "virtual", too. The Z boson also prefers to produce lighter quarks or leptons as it decays, so there is some accounting to do for the phase space suppression; otherwise, one might expect one Z boson in ten to give two tops.
2b - A W boson (the charged brother of the Z, also discovered in 1983) may produce a top- antibottom pair in its decay, if it carries enough energy (a high virtuality, that is); the W weighs 80.4 GeV normally, so we are again talking about a very peculiar W boson. The W has an advantage, however, because it only produces one top, so it does not require to have an energy above twice the top mass: 180 GeV may be enough, since the bottom quark weighs less than 5 GeV. But then, the W can only produce one top quark at a time, and not a pair!
Okay: the three above (notice that they are labeled 1) and 2a), 2b) to stress they belong to two different classes) are the blocks we may use to cook up particle reactions capable of yielding top quarks. Now, the most probable process yielding top quarks at a hadron collider is the first we discussed, for a simple reason: the colliding protons contain gluons aplenty, while W and Z bosons are more rarely found inside them! This is equivalent to saying that strong interactions are strong, and weak interactions are weak: the latter being weak is the result of the less probable emission or absorption of weak bosons.
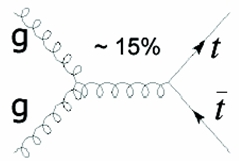So we may have top-antitop production by gluon-gluon fusion, as shown on the right. In the diagram, you should realize that time is taken to flow from left to right, spatial distance is on the vertical axis, and that each line represents the propagation of one particle in space-time. One would then read it as follows: two gluons get closer until they hit each other; they fuse together into a third, which propagates for a while in time; then this gluon "splits" in a top-antitop pair, with the two final state quarks getting away from the creation point. I hope the picture is clear enough now, because I am not going to provide the same detail for the other reactions I want to show below (please ignore the 15% label, which is only relevant for Tevatron collisions).We may have the same top-antitop final state produced by a quark-antiquark annihilation process, such as in the diagram on the left.
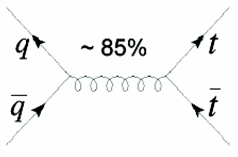The one shown is still a "gluon-splitting" production of the top quarks; the difference with the former process is just in the two catalysts, quarks in this case. (Again, ignore the 85% label here).We might also think to produce a top-antitop pair with the intercession of a Z boson; bear in mind that this is way less frequent, as noted above.
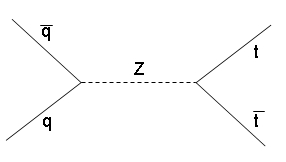The process is shown in a very lousy diagram I drew myself with powerpoint on the right.Finally, one might even cook up a top pair with the help of two W bosons, but this is doubly as rare as the Z exchange diagram.
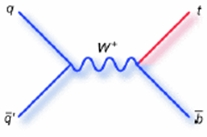You can see it in the more colorful diagram on the left.And now, what about the production of three top quarks (or a top-antitop pair plus a single additional top quark) ? The authors produced some neat diagrams, so I will avoid fiddling with vector graphics and steal them from the source (I should really learn to work with the tools they use to produce these diagrams!):
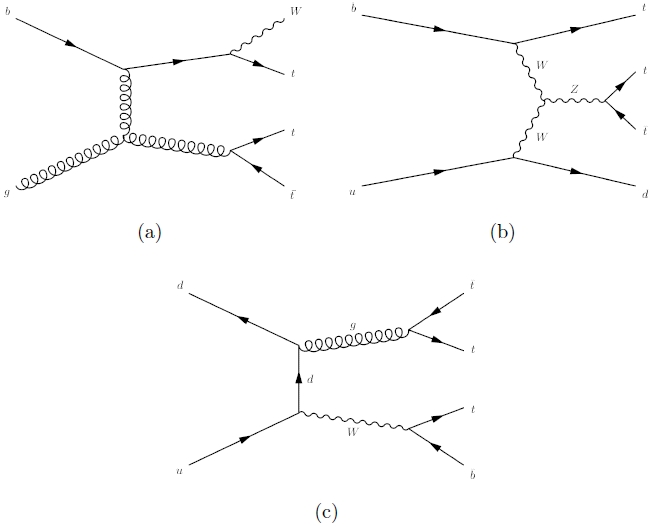
Some quick-and-dirty explanation is required to figure out what is going on in the diagrams above:
(a) A b-quark exchanges a gluon with another gluon; the b-quark then "radiates" a W boson, turning into a top quark; meanwhile, the other gluon splits in a top-antitop pair.
(b) A b-quark interactis with a u-quark by exchanging a W boson, and in so doing the b-quark turns into a top quark (this change of species is most frequent with b-quarks, but also d- and s- quarks can do it in principle, although much less frequently). The W boson emits a Z boson, which then materializes a top-antitop pair.
(c) two light quarks interact, emitting a W boson and a gluon. The gluon splits in a top-antitop pair; the W boson produces a third in its decay.
As you see in the diagrams (a), (b), and (c) above, three tops can only be the result of the combined action of weak and strong interactions. Weak interactions are essential if one wants a odd number of top quarks, because strong interactions cannot produce top-ness: they can only produce tops in particle-antiparticle pairs, such that the total change of top-ness from initial to final state is zero (anti-top quarks carry the opposite amount of top-ness than top quarks do).
Sizing up multiple-top quark production at the LHC
The diagrams we have seen above are only there as an example: the authors of the paper are careful to point out that there are hundreds of similar diagrams one is required to compute and sum together, in order to give even the roughest estimate of the total rate of three-top production. They did precisely so, and the results are shown in the figure below.
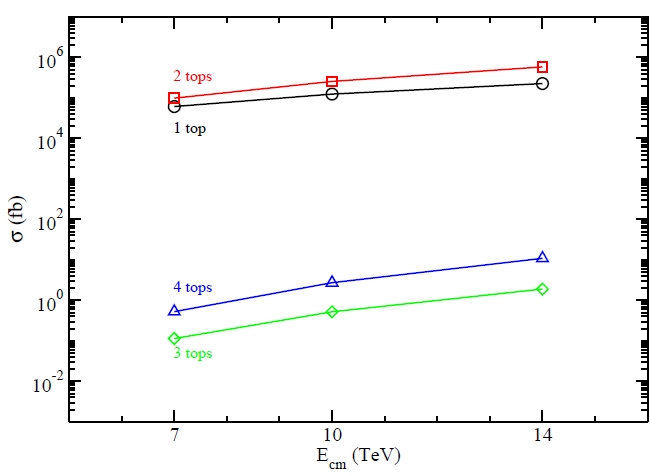
Here you can see, as a function of the center-of-mass energy provided by the LHC collider (7, 10, or 14 TeV), the cross-section for producing one, two, three, and four top quarks. The cross section is a number proportional to the rate of the process, so you can think of the vertical axis as simply the production rate of the various reactions. There are many things to note in this simple diagram. Let me list them in good order.
1. Producing two tops is easier than producing one, and producing four is easier than producing three! This occurs because of the weakness of weak interactions, and it is so despite the fact that each time you add one top quark to your request of a final state, the energy of the colliding quarks or gluons (the part of the projectiles that actually give rise to the energetic collision) has to increase by at least 172 GeV in order to enable the process. 172 GeV are a lot of energy even for a 10-TeV collision, because most of the total collision energy does not go into the "hard subprocess" which is what produces the new states of matter: most of the energy is in fact carried away by the remnants of the two protons.
(Maybe I need to explain this in more detail with an example: what you do when you collide two protons is like to launch a handful of sand grains against another handful: most of the grains will pass unscattered, and only a few grains will hit others head-on. We are interested in the energy of these few head-on collisions, which will not be the total energy of the two handfuls, but a much smaller part.)
2. The growth with collider energy (a.k.a. the positive slope of the curves) of the 1-top and 2-top processes is much milder than the growth of the 4-top and 3-top processes: this is again due to the fact that it is rare to produce a very energetic collision (one releasing enough energy to produce 3 or 4 tops), so these more infrequent energetic processes benefit more of a doubling (from 7 to 14 TeV) of the total proton+proton energy. Explaining in detail why that is so would require me to delve in what we call "parton distribution functions", which basically describe the probability densities of finding quarks and gluons with a given fraction of the total proton energy. If you care about this, ask it in the comments thread below and I will provide a better explanation.
3. There are almost 5 orders of magnitude between the 2-top and the 4-top production rates, and over 5 between the 1-top and 3-top rates. This is due both to the rarity of energetic collisions, and to the rarity of two simultaneous materialization of heavy quark pairs. Three-top production is 100,000 times less frequent than single top production!
4. The three-top production is the rarest one: at 14 TeV energy, the rate is of one event per inverse femtobarn of collisions. What that means, at the LHC, is roughly one three-top production event per week of running, when the machine will finally achieve its top energy and power.
New Physics in multi-top production ?
Of course, seeing triple top production would be nice even in the absence of new physics: take the search for single top at the Tevatron as an example... Dozens of physicists spent several years of their life to confirm that the process occurs as predicted by weak interactions in the Standard Model. But the paper makes an even stronger case for a search of three-top events at the LHC by considering two possible new physics scenarios. One is Supersymmetry which, with a particular choice of its defining parameters (called "focus point" by experts) might enable decays of gluinos yielding odd numbers of top quarks:
"A feature of this benchmark point is that the gluino mass, Mg=782 GeV, is less than that of the squarks. Gluino decays to quark-squark pairs [...] are kinematically inaccessible, opening up three-body decays via virtual squarks [...] These decays can result in both single- and double-top final states with considerable branching fractions of 10-20% [...] Because gluinos are strongly interacting, the production of gluino pairs at the LHC will be very large, typically several hundred femtobarns. With one gluino decaying to a single top [...] and the other to a top pair [...], the rate of triple-top events can therefore be quite large in the MSSM in this region of parameter space."
So if Supersymmetry -and in particular, its variety called "focus point" of the MSSM, the minimal supersymmetric extension of the Standard Model- is the correct theory of nature, we should expect an enhancement of events with three top quarks at the LHC. This, alone, is a reason for looking for such events. But there is more. Here we appreciate the creativity of theorists:
"The major limitations to the rate of triple-top production in the Standard Model [... is the] initial state b-quark needed to create the single top [...]. Models that can produce this single top with greater ease should therefore have a larger triple-top signal as well. An example of one such model is the addition ofa U(1)' symmetry in which a leptophobic Z' couples the top directly to the u-quark."
Please ignore the technicalities in the quote above, and just note that the model that is being mentioned is quite odd. There is a reason for considering such oddity, as the authors are quick to point out:
"This model was discussed [...] as a candidate for describing the observed two-sigma deviation from the Standard Model prediction of forward-backward asymmetry in the top-pair signal at the CDF detector of the Tevatron collider."
Hmmm. Let me fish that result out, to see just how optimistic these theorists have been in considering a rather odd-looking model based on a two-sigma deviation.
A Digression: The CDF top-antitop Asymmetry Anomaly
Two-sigma asymmetry in top quark production ? I do not remember such a thing, and that is strange, because I am quite interested in two-sigma effects -I tend to not let them pass by without an article in this blog. Further, I have certainly signed the publication that Barger et al. quote in the article we are discussing... I am intrigued!
Okay. Below, extracted from the 2008 CDF publication, is the plot on which the CDF collaboration measures the forward-backward asymmetry of top-quark pairs. Unfortunately, the analysis is very nice, but I have no space to discuss it in any detail here. Let us have a look at the result.
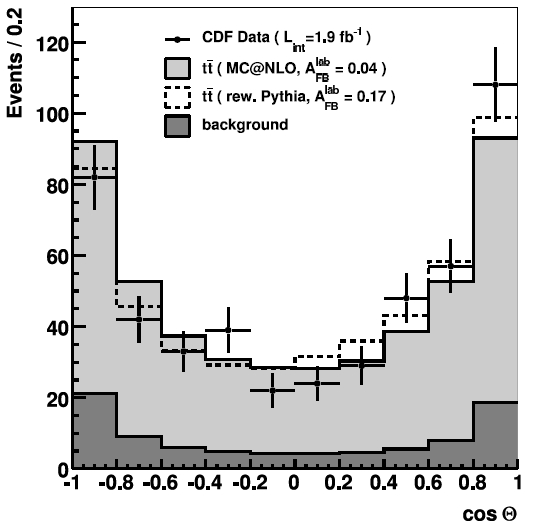
This histogram shows a "top production angle variable", the cosine of an angle theta describing the production of top quark pairs. The black points show the distribution of the data, while in light grey you can see the predicted top distribution, and the darker grey show the background. The points do show a slightly asymmetric distribution in cos(theta) with respect to the sum of the two histograms, but I doubt that it constitutes a two-sigma effect (which, for non-experts, is a difference whose probability of occurring by chance, once accounting for measurement uncertainties, is of 3% or less).
The measurement, one should note, is not terribly sensitive on any given production asymmetry: the dashed line, which shows the prediction for a 17% asymmetry, is not very distant from the histogram. From the analysis of the data, my collaboration assessed the result as follows (I am quoting from the CDF paper now):
"In conclusion, we have measured a forward-backward and (equivalent) charge asymmetry in a strong process at high energy using reconstructed top-antitop events produced in proton-antiproton collisions [...] We find forward-backward parton-level asymmetries of 0.17+-0.08 in the proton-antiproton frame [...] Our results [...] are consistent (<=2 sigma) with the small (~0.05) charge asymmetry expected from QCD, and they disfavor exotic sources of top quark production with significant negative A_FB values."
So CDF thinks the observed distribution is in good agreement with the Standard Model (here what counts is the part called "QCD", for Quantum ChromoDynamics, which governs the subset of Standard Model interactions called "strong interactions"), and says that the measured asymmetry is a "less than or equal to" 2-sigma effect.
So, never mind taking this as an inspiration for model-building; but there remains the question: what would be the asymmetry for the model that the theorists have chosen in their paper ? I could not find an answer in the article by Barger et al.
Conclusions of the study
Anyway, let us look at the conclusions of the admittedly very interesting article I have discussed today: these can be summarized in a graph showing the predicted rate of three-top events in the two new physics models, compared with the Standard Model prediction. Check it out in the figure below.
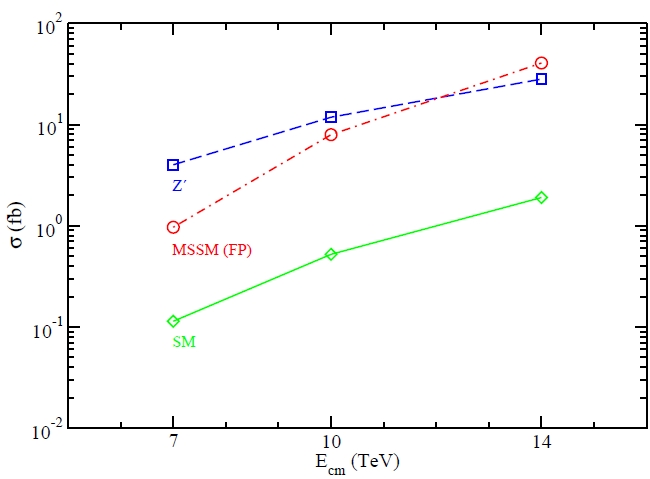
Interesting! The two new physics models predict rates over one order of magnitude larger than the Standard Model for three-top production. Definitely, this is like measuring a one-gram angel on the shoulder of an ant weighing a tenth of a gram... It should be feasible!
I love physics models that offer their chest to the sword. They have the courage to put themselves to the experimental test, and live in glory or die in perennial oblivion. These models do precisely that: give LHC a few years to collect the data, and they will be tested for good. Quite different from landscape string theories, don't you agree Lubos ?
Comments