Decision trees are one of the many players in the booming field of supervised machine learning. They can be used to classify elements into two or more classes, depending on their characteristics. Their interest in particle physics applications is large, as we always need to try and decide on a statistical basis what kind of physics process originated the particle collision we see in our detector.
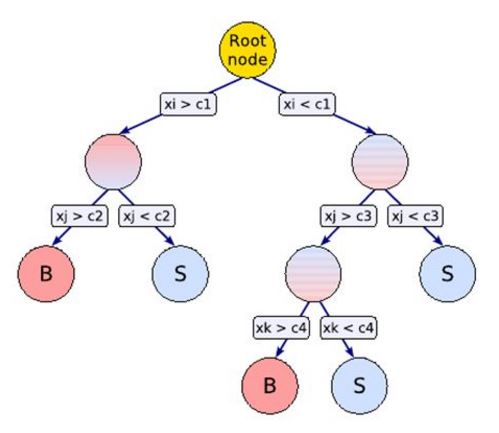
In a decision tree with a binary output (two classes), the various characteristics of the elements (features) in a training set are considered in succession, finding a way to decide whether an element is of class A or class B based on the observed feature. Of course this is only the basic element of more complex structure, like random forests of trees and boosted trees that constitute the cutting edge of this kind of algorithms. In random forests, a number of different trees is constructed, each using only a subset of the possible features; then the trees output is combined, obtaining a more stable and performant classification. In boosted trees, a boosting is applied by letting the algorithm teach itself how to give more weight to examples that were misclassified in a previous learning cycle.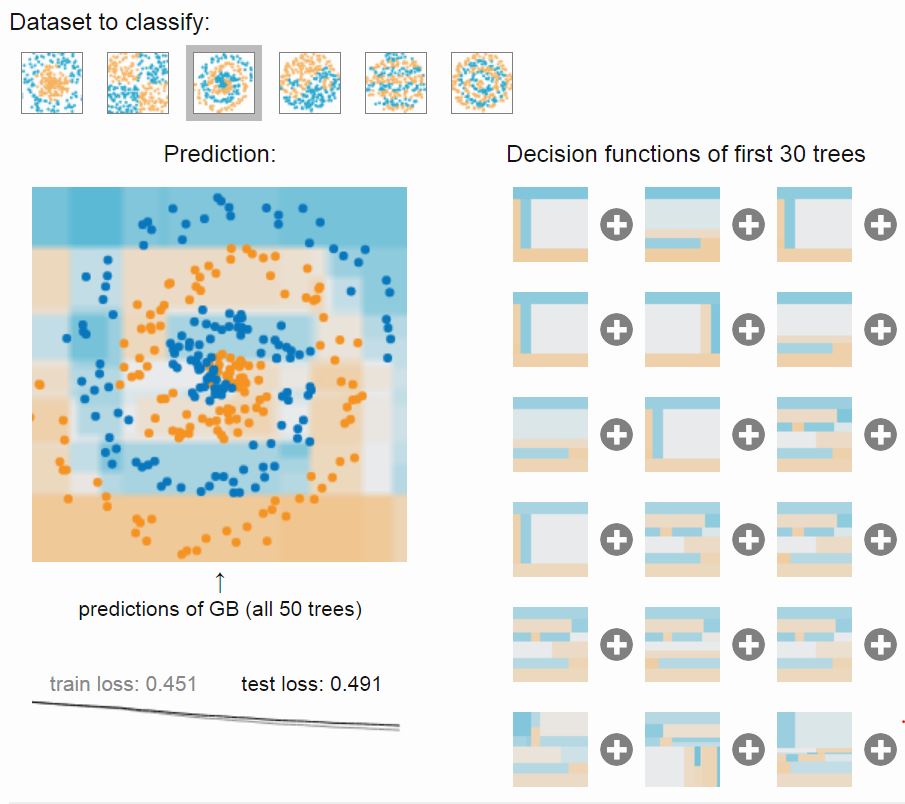

There exist a wealth of software tools for decision trees. There are even online demonstrators, such as this one (see also the screenshot on the right) - you can play with the features you wish to consider for the elements to be classified, and watch as the algorithm creates trees and constructs its output. However, in the attempt to create something visually attractive and easy to grasp that could explain the concept of classifying elements, having in mind laypersons and kids, I came up with something different.

The idea is to construct a tilted board, where balls of different colour and characteristics are fed in from atop. The ball falls down by traversing different "modules" where their features get appraised by simple mechanical devices, and as a result move to the left or to the right as they fall. Eventually, balls of the two colors should accumulate preferentially on different sides. 

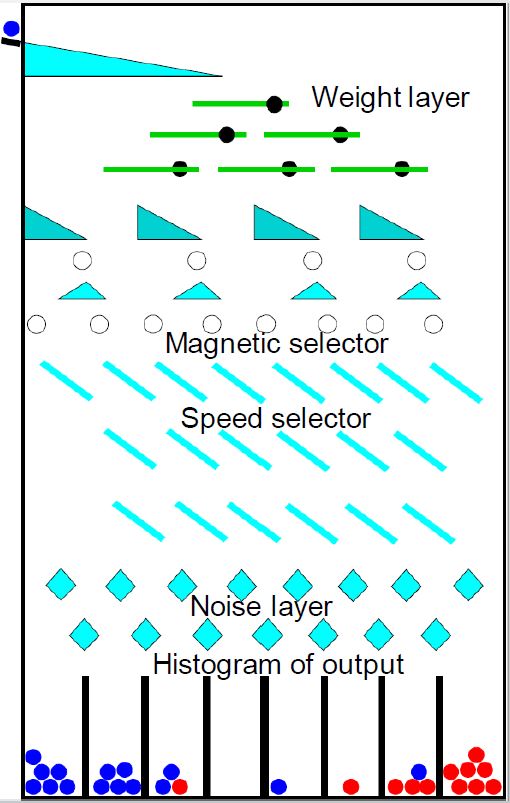A simple implementation consists in considering balls of different weight, magnetic properties, and speed of moving through the slopes. In the design on the right there are three "selector layers" that operate this. The top one is a set of balances that let heavy balls tilt them such that they slide to the left, while lighter ones slide to the right. The middle one uses magnets to steer iron balls toward the left. The bottom one is a set of slides with holes: faster moving balls will jump the holes and move preferentially to the right.

I am considering constructing this device for an "Open Day" of the European Union, which will take place in Brussels on May 6th - the ITN network I coordinate has been invited as a potential contributor, to create a stand where we explain our research. I would like to ask you if you know of something like the above already built - so that I can eventually borrow ideas or even the whole thing - or if you have ideas on how to improve the above concept. Thanks!

Update: I realize that it would not be very complicated, although more technically challenging, to design a version of the above that explains the concept of "Random Forests". The idea would be that the above design is replicated into N such devices in parallel, in each instance changing selectors or inverting their order etc. Then, rather than one single ball, M (<N) balls are injected in a random selection of the devices. At the bottom of it, a "majority" device would give an output to the left or to the right, depending on how many inputs it received. One can probably further improve it in many ways...