Do you like Thomas Pynchon, but are you stumped by the crazy turn-of-the-century science in his latest novel, Against The Day
OK, it's not just for Pynchon readers - I think this science is fun even if you haven't read Pynchon. So check out part one, about how Michelson and Morley realized that something wasn't quite right with the 19th century understanding of space and time:
Thomas Pynchon is well known for the dense and obscure references to history, pop-culture, and especially science in his novels. His recent novel Against The Day
Pynchon takes the science of this period and incorporates it deeply into the language and structure of Against The Day
One reviewer claimed that a new generation of writers has a "grasp of the systems that fascinate Pynchon -- science, capitalism, religion, politics, technology -- [that] is surer, more nuanced, more adult and inevitably yields more insight into how those systems work than Pynchon offers here." When it comes to science at least, this claim is not true - Pynchon's achievement in Against the Day proves that he is peerless as a poet who can mine science for gems of insight and set them into the context of the humanity that is the ultimate concern of his novels.
My goal here is twofold: first, to show how Pynchon goes beyond using science as simply a backdrop, or a way to show off his amazing erudition - he weaves scientific concepts into the language and structure of his book; and second, to lay out a primer on the basic scientific ideas so that readers of Against the Day can make their own discoveries about the novel.
There are three main topics that I'll cover eventually: the Michelson-Morley experiment and the breakdown of classical physics, the development of vector analysis and the eclipse of quaternions, and finally, Riemann surfaces. These cover most of the scientific references in Against The Day
It is also important to note the science Pynchon did not include in the novel - other important advances were being made at the time, by some of the same characters, advances that Pynchon hardly mentions such as those in statistical mechanics (and even Pynchon's signature topic, entropy) made by J.W. Gibbs. In this book, Pynchon has chosen to focus on space, time, and light.
The Michelson-Morley Experiment and the Failure of Classical Physics
The Michelson-Morley experiment (actually, a series of experiments performed over several years) was one of the definitive experiments providing physical evidence of the inadequacy of classical notions of space and time. The attempts to deal with the negative results of this experiment eventually led to Einstein's theories of special and general relativity, which are based on a completely different and very strange new way of viewing space and time. This new outlook has since been proven beyond any doubt by decades of experiments.
Early on in the book, Pynchon drops clues that the Michelson-Morley experiment is important for many of the themes that we'll find throughout Against The Day
"Mr. Rideout, we wander at the present moment through a sort of vorticalist twighlight, holding up the lantern of the Maxwell Field Equations and squinting to find our way. Michelson's done this experiment before, in Berlin, but never so carefully. This one could be the giant arc-lamp we need to light our way into the coming century." (p. 58)
At the time this conversation takes place, in 1887, Michelson had improved on the design of his interferometer (the device used to carry out the experiment), so that it was easily sensitive enough to definitively answer the question he was posing. The negative outcome of this experiment was a major stepping-stone towards the development of a new understanding of light, space, and time. To see how this new understanding arose, we have to first understand the questions in classical physics that led to the Michelson-Morley experiment.
I. Classical Relativity
Albert Michelson began his famous series of experiments because the laws of classical physics, which in general were spectacularly successful, were running into trouble in one critical area: moving reference frames. Although we not may use the term 'reference frame' very often, we deal with moving reference frames in our everyday experience. As we have all experienced, Newton's laws of motion don't depend on whether we're on the ground or in a vehicle moving at a constant speed (constant here is an important qualifier). For example, you can play tennis on a steadily moving (that is, non-accelerating) cruise ship just as easily (or not so easily, in my case) as you play tennis on land - you handle yourself and the tennis ball the same way. Or, if you're on a steadily moving (again, non-accelerating) train, you can bounce a ball against the floor, and it behaves just as if you were bouncing it on the floor of your kitchen back home. The ball bounces straight up and down, keeping up with the train as you bounce it, as long as the train does not suddenly accelerate. From your perspective, or reference frame on the train, Newton's laws of motion, which govern the movement of the ball you are bouncing, are exactly the same as they would be if you were standing outside on the ground. Newton's laws apply equally well to moving and stationary reference frames (as the moving frame is not accelerating).
To someone standing on the ground outside of our hypothetical train, watching you bounce the ball as you go by, the situation looks a little different, but still completely in accordance with Newton's laws. This outside observer sees that the ball isn't going straight up and down; it's also moving forward with you and the train, nevertheless, the ball is also obeying Newton's laws from this outside perspective. All of this is common sense and intuitively obvious to us, but one can also show that it works out mathematically as well.
While this phenomenon is true of Newton's laws of motion, the classical laws of electricity and magnetism do not hold in different moving reference frames. To see what this means, we can use one key example: light. Maxwell's classical laws of electromagnetism imply that the speed of light is constant (in a given medium like a vacuum - light moves at different speeds in different media like water or air). If we simply treat light the way we treated Newton's laws in our above examples of the cruise ship or the train, the speed of light would not be constant for observers in different moving reference frames. If I'm standing on the ground watching a pulse of light go by, I would see that it's going at 300,000,000 meters per second (m/s). Someone on a train moving at 50 m/s, watching that same pulse of light go by, would perceive the light to be moving at 299,999,950 m/s. (This difference is of course, too small to be perceptible to unaided human senses). In this case, the speed of light, unlike Newton's laws, is not constant for observers in different reference frames, and thus the laws of electromagnetism would be different, depending on your frame of reference. So, while Newton's laws are the same whether you're playing tennis on the ground or on a cruise ship, this appears to not be true for Maxwell's laws of electromagnetism. Maxwell's laws would thus not be the correct laws to describe the behavior of light in moving reference frame. (At this point, we should be careful to remember that these are just theoretical considerations - we haven't discussed any actual experiments to really determine what happens with Maxwell's laws on a moving train or a cruise ship.)
Physicists in the late 19th century were well aware of this conundrum. They believed that there had to be one universal frame of reference where the speed of light was constant in any direction, in which Maxwell's laws of electromagnetism were perfectly valid; all other objects in the universe moved relative to the absolute space of this universal reference frame. This was called the aether frame of reference - aether was the stuff (although what kind of stuff, nobody knew) through which light supposedly propagated, much like sound must propagate through air or some other medium. The earth therefore moved relative to the stationary aether, much like a train moves relative to the 'stationary' earth. If this was in fact true, that the earth moves relative to the aether, then this movement should be detectable by experiment. And here is where Michelson and Morley come in.
II. Michelson and Morely Attempt to Measure the Absolute Speed of the Earth
Albert Michelson (who, like many characters in Against the Day, grew up in mining towns) and Edward Morley developed an extremely sensitive instrument to measure the speed of the earth relative to the hypothesized aether. The reasoning behind the experiment goes something like this: if light propagates at a constant speed through the aether (at 300,000,000 m/s), and if the earth moves at a certain speed relative to the aether (at, say, 30,000 m/s), then light moving in the same direction as the earth should appear to move more slowly to an observer on the earth - the speed of light in the aether, minus the speed of the earth. It's like driving on the highway - if you are going 60 mph and driving behind a car going 90 mph, then from your perspective the car in front is moving away from you at 30 mph. Michelson and Morley measured the speed of the earth relative to the aether and came up with a disturbing result - relative to the aether, the earth was not moving at all.
I'm won't describe exactly how the Michelson-Morley experiment worked - good explanations can be found in a physics textbook or a Google search. However, the basic setup of the experiment has a connection to some of the plot structure in Against the Day, as well as to the themes of double refraction and bilocation.
In the experiment, a light beam is split into two separate beams, which travel away from each other at a 90˚ angle, are reflected by mirrors, and then travel back and meet up, at which point they are either in phase or out of phase with each other (see the diagram below). If the earth is moving relative to the aether, the different light beams will travel different distances, and come back out of phase with each other.
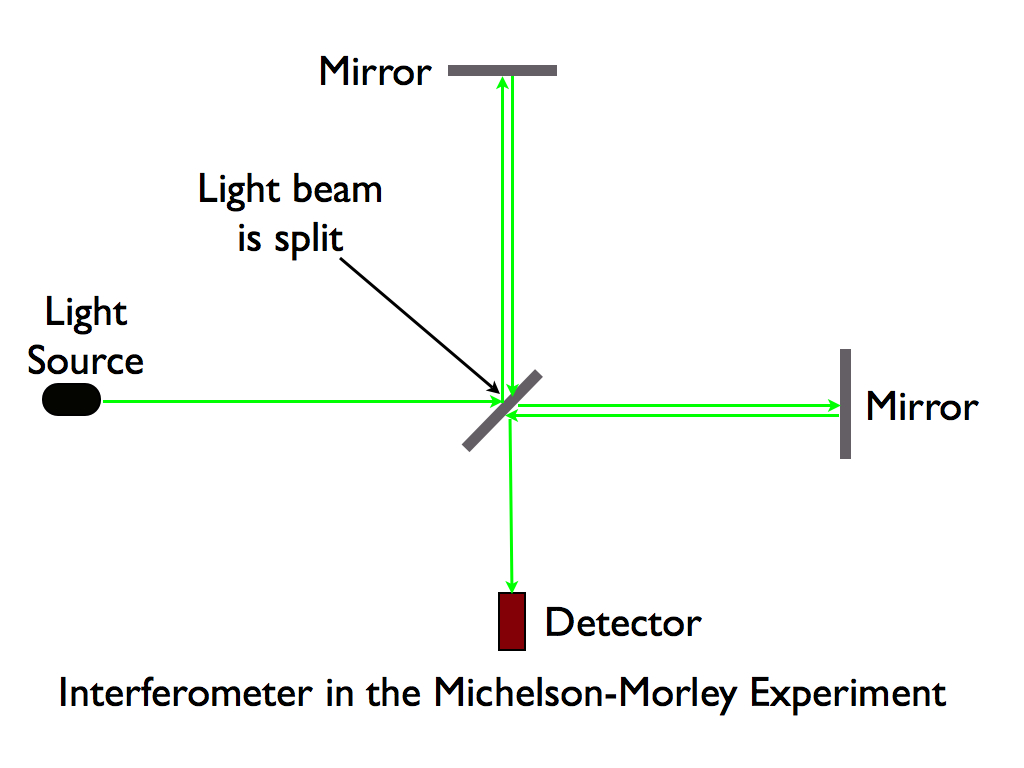
Pynchon hints that there is a connection here with bilocation and double refraction, as well as human Michelson-Morley experiments (such as, possibly, when characters split up, go on long journeys and meet up again in or out of phase with each other in some way). There are some critical passages beginning on p. 61, where Merle "got the idea in his head that the Michelson-Morley experiment and the Blinky Morgan manhunt were connected." Blinky is referred to as a "human interferometer" or "A double-refractor, for that matter." (p. 62) In one of the earliest examples of bilocation in the book, Merle suspects that Morgan and Morely are the same person:
"... suppose when they split that light beam, that one half of it is Michelson's and the other is his partner Morley's, which turns out to be the half that comes back with the phases perfectly matched up - but under slightly different conditions, alternative axioms, there could be another pair that don't match up, see, in fact millions of pairs, that sometimes you could blame it on the Aether, sure, but other cases maybe the light goes someplace else, takes a detour and that's why it shows up late and out of phase, because it went where Blinky went when we was invisible, and-" (p. 62)
The connection between Iceland spar and the Michelson-Morley experiment is made more explicit later in the book, where the Cohen explains to Lew Basnight that his goal is to eventually be able to pass through Iceland spar, "which is an expression in crystal form of Earth's velocity as it rushes through the Aether, altering dimensions, and creating double refraction...." (p. 688)
Pynchon plays with this idea at multiple places throughout the book. He also includes elements of an aether culture - worshippers who show up for the Michelson-Morley experiment (p. 59-60), as well as hints of a whole science of aether weather, with which the Chums of Chance seem to be involved - a network of ships and balloons to monitor the ether is hinted at on p. 60. (Historically, people did in fact come up with elaborate ideas using putative aether behavior, such as vortices, to explain physical phenomena.)
Returning to Michelson and Morley - the results of their experiment were negative. They could detect no movement of the earth relative to the aether. Over the next several decades, scientists came up with various explanations for the negative result. One explanation, mentioned in Against the Day, is that the earth drags some of the aether along with it (and thus the earth isn't moving relative to the dragging layer of aether, so you don't detect a change in the speed of light). One of Pynchon's characters draws an analogy between this explanation and the dimples on a golf ball, and the lift of the golf ball through the air and the lift of the earth through the aether. [I'm sure Pynchon includes more, but I'll have to pick that up on a second reading.]
III. Revising Our Notions of Space and Time
One possible solution to handle the negative result of the experiment was to try to modify the laws of electromagnetism. Maxwell's equations were quite young compared to Newton's laws, so it seemed obvious that the problem was with Maxwell and not Newton. However, it became clear that Maxwell's laws were in fact correct, and eventually (as Einstein's theory of special relativity became accepted), that light traveled at a constant speed in any non-accelerating reference frame - not just in one universal aether reference frame. This means that whether you are standing on the ground or traveling at 100,000,000 m/s in a (currently fictitious) space ship, a light pulse will always appear to be traveling at 300,000,000 m/s. To go back to our highway analogy - you're going 60 mph behind a car going 90 mph, and instead of appearing to move away from you at 30 mph, the car appears to be going 90 mph away from you. The implication of this very weird phenomenon is that our everyday ideas about space and time are not correct.
Maxwell's equations weren't the problem - Newton's laws were. The physicist Henri Lorentz, between 1895 and 1905 proposed that objects in motion experience length contraction and time dilation, a proposal (in mathematical form) which could account for the results of the Michelson-Morley experiment. In other words, as you move faster and faster, space (from your frame of reference) shrinks in certain directions, and time slows down. If you go through Lorentz's math (known as the Lorentz tranformation), you see that space and time components, in one reference frame, get mixed together when you move to a different reference frame - space and time are not separate, they depend on how one is moving.
We can think about this by drawing an analogy with the video game Frogger In the game, you get a frog across the road by moving it left, right, up, or down. Now, imagine it this way - instead of having the frog face directly across the road, it's rotated at a 45˚ angle to the right, facing diagonally across the road - the frog's reference frame has rotated. 'Up' now (in this reference frame) is the equivalent of some 'up' and some 'right' in the original reference frame. 'Up' in one reference frame is a mixture of 'up' and 'right' in another.
The analogy isn't perfect (going over the math is the best way to look at it), but that's roughly what's going on with space-time. Instead of 'up' and 'left' in Frogger, we have three space dimensions and one time dimension, and how you perceive the combination of those dimensions depends on your frame of reference. (Unlike in our hypothetical game of Frogger, where we just changed the reference frame by rotating the frog, changing space-time reference frames depend on motion - the faster you move, the more slowly time passes, etc.)
So how we perceive space and time depends on how we are moving. (Does the eternal youth of the Chums of Chance somehow depend on their motion?) But no matter how we move, no matter what our reference frame, light moves at the same speed for all of us.
Pynchon makes a lot of this material, playing with both the language and the concepts.
Move on to part 2...
For further reading:
Feynman Lectures on Physics, Vol. 1 chapter 15
Modern Physics for Scientists and Engineers, by John Taylor and Christopher Zafiratos.
The Fabric of the Cosmos, Brian Greene.
Comments