The Fire In The Sky
Understanding climate science requires a cross-disciplinary approach. I am trying to explain in this series the most important aspects of the relevant sciences. This is the 4th part of the mainly astronomical section. In part 2, I introduced the idea of, in a manner of speaking, building a model of our earth-moon-sun system. In part 3 I continued with a discussion of seasons and their primary astronomical causes. Here I begin to discuss the astronomical factors affecting how much heat the earth receives from the sun annually.
New readers may wish to start at Understanding Climate : #1 - Components Of Climate.
--------------------------
The Fire In The Sky
Without the sun, we wouldn't be here to discuss climate. The earth warms in the daytime and cools at night. In a perfect universe these two heat flows would balance, and the earth's temperature would be constant, averaged over the entire surface, for every year.
Disregarding for now any influences from earth itself, let us examine what astronomical science can tell us about the average annual heat input to the earth. I shall begin by explaining an easy way to determine average insolation.
Insolation - solar heat at earth's orbit
Insolation is the total heating effect of the sun over the daylight side of planet earth at all radiation frequencies. In order to determine the annual insolation we don't have to do any complex maths. We don't have to consider the varying angle at which radiation strikes the earth between equator and poles. Why use complicated methods when there is an easier one?
Think of the mechanism of an eclipse - a way of shutting out the sun. If a disk the same diameter as earth could be placed just touching the equator and at right angle to a path between the centres of the sun and the earth, then it would block all radiation from the sun.
Such a disk would be exactly the right size to block all of the radiation that would otherwise fall on earth. It follows that it intercepts, and therefore itself receives, exactly the amount of radiation that the earth would have received in its absence. So: instead of integrating all those diminishing amounts of radiation over a hemisphere, we can just work out the area πr2 for the required disk.
The top of the atmosphere
Insolation is measured at the top of the atmosphere, so although we are for now disregarding the effect of the atmosphere we must include its depth. The problem is: where is the boundary between earth and space? That is a difficult thing to pin down and there are various lines drawn for various purposes. To help build my written model of climate processes I shall use the Karman line - the height at which the air is so thin that an aircraft, in order to generate lift, would have to travel faster than the orbital velocity for that height.
The Karman line is at 100 kilometers - 62 miles - above the surface. The Karman radius of earth, the radius over the aerodynamically useful atmosphere is 6478 kilometers, about 4025 miles. This gives us an area of disk, πr2 , 131,835,314,495,443 m2 needed to block all insolation.
The solar energy falling on each square meter of such a disk is the same as the solar constant: 1368 W/m2. The solar constant is an average over a year of values measured by satellites. Multiplying area by the solar constant we get 180,350,710,229,765,477 Watts per annum - 1.803×1017W - being intercepted by planet earth. This result compares well with published figures which appear to omit atmosphere, using surface radius to calculate annual insolation.
Please note that the figure for annual insolation is a whole globe amount. It is the amount of sunshine which would be absorbed in the course of a year by a black disk with earth's Karman radius and tracking completely around earth's orbit so as to block all radiation from reaching the planet. The global annual value needs no adjustment to allow for day and night. The ring below shows day on the inside and night on the outside. The ring is a virtual ring - it illustrates the orbit of a disk - a true ring would collect insolation constantly, not in daily increments.
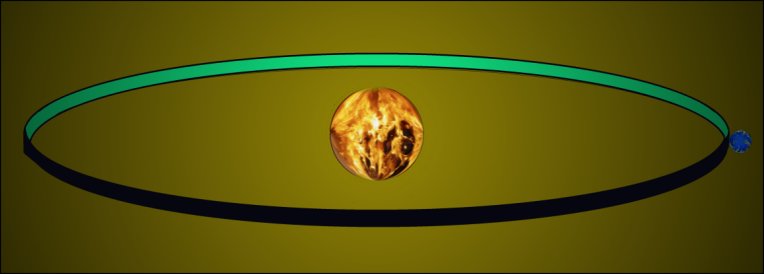
If the ring illustrated above existed, it would absorb radiation and then re-radiate it. It would glow on both sides in the infra red. It would reach some equilibrium temperature at which the amount of heat radiated into space was identical in energy to the amount of radiation of all frequencies received from the sun. And from empty space.
The temperature of space
How can empty space have a temperature? We don't need to delve into cosmology or quantum physics for an answer that anyone can readily understand. If space was full of dust there would soon come a time when each speck of dust was absorbing and emitting radiation at equilibrium with every other average speck of dust in its region.
In that situation the temperature of space would be pretty much the same as the surface of the sun. There would be no inverse square law at the astronomical scale: the temperature of space at earth's or even pluto's orbit would be much the same as the sun's surface.
Fortunately space is nearly empty. So empty that the temperature of space is about 2.725 K. The temperature of space - the cosmic cold - is vital to our planet's temperature control. The amount of energy which a body can radiate away depends on the difference in temperature between the body and its immediate surroundings. Even while a body is radiating heat, its surroundings will always be radiating some amount of heat back at the body.
In physics, energy isn't lost, it is always converted in some way. Fortunately, as far as building a climate model goes, we can just assume that heat lost to space disappears from our model. There is no problem with this approach: our planet can dump heat into space for as long as there is a planet earth with excess heat and a cooler cosmos to dump the heat into. We shall see later why dumping heat into the atmosphere doesn't work the same way.
The next topic in this series will discuss the ways in which the annual insolation varies over time scales ranging from minutes to millenia.
Further reading / related:
http://acrim.com/TSI%20Monitoring.htm
http://www.grc.nasa.gov/WWW/K-12/Numbers/Math/Mathematical_Thinking/esti...




Comments