Today's underwater acoustic communication relies on scalar sensors to measure the pressure of the acoustic field. However, "a vector sensor is capable of measuring important non-scalar components of the acoustic field such as the particle velocity, which cannot be obtained by a single scalar pressure sensor" according to Ali Abdi, PhD, associate professor in the department of electrical and computer engineering at NJIT.[1]
Abdi and his team present in "A New Vector Sensor Receiver for Underwater Acoustic Communication" their novel idea of using vector components of the acoustic field to detect transmitted data as sensed by a vector sensor at the receiver. A vector sensor can measure both the scalar and the vector components of the acoustic field at a single point in space. Therefore a vector sensor can serve as a compact multichannel receiver.
To derive the basic system equations for data detection, they consider a vector sensor communication system in an underwater channel. The figure here shows this simple system of one transmit pressure sensor (a fancy dark dot) and one reception vector sensor (a dark square) to measure the pressure and the y and z
components of the particle velocity. In other words, we see a basic two-dimensional, 1x3 single-input multiple-output (SIMO) system. Additional pressure transmitters would make up a multiple-input multiple-output (MIMO) system.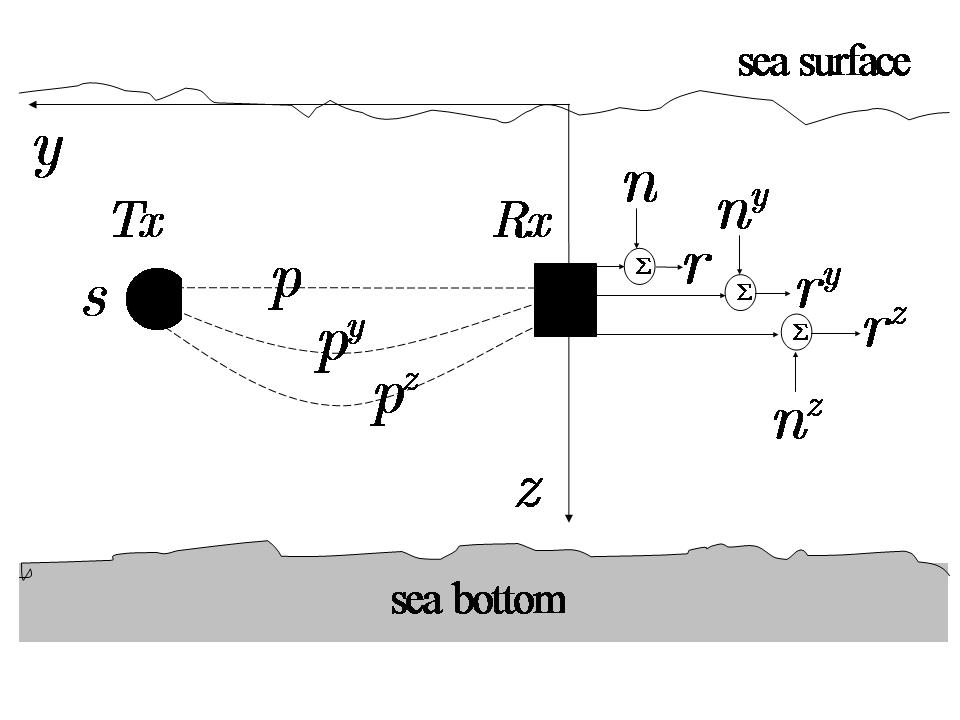
(Source: A. Abdi)
There are three channels in the figure: "the pressure channel p ,represented by a straight dashed line, and two pressure-equivalent velocity channels pz and py , shown by curved dashed lines. To define pz and py , we need to define the two velocity channels vz and vy , the vertical and horizontal components of the particle velocity, respectively."
The received pressure signal at Rx in response to the signal s transmitted from Tx can be written as r=p⊕s+n, where ⊕ and n are convolution in time and additive ambient noise pressure at the receiver, respectively. Abdi et al apply the first principles to obtain the key system equations as
r=p⊕s+n, ry=py⊕s+ny, rz=pz⊕s+nz
where three output signals r
, ry and rz are measured at a single point in space.
The rest of the paper proceeds to channel equalization using these sensors and signal and noise power characteristics in such sensors. The performance of a vector sensor equalizer is determined and compared with single and multiple pressure sensor receivers.
Extensive Monte Carlo simulations are provided under different propagation scenarios.
Overall, Abdi et al demonstrate the usefulness of a vector sensor as a compact multichannel equalizer with elegant mathematical rigor. That should be fine news to commercial and naval underwater communication interests. Applications might revolutionize monitoring activities and data communication in the vast oceans beyond what is possible today.
Reference
[1] A. Abdi, H. Guo and P. Sutthiwan, “A new vector sensor receiver for underwater acoustic communication,” in Proc. MTS/IEEE Oceans, Vancouver , BC, Canada , 2007




Comments