It is convenient to think of cells as the units of life, and to associate biological complexity with the cooperation of cells in multi-cellular organisms. Yet, we must delve into its inner workings to understand the life force that seems to compel cells to grow, metabilize, and divide. When we zoom into the atomic level, we see that there is no force at all but only the sum molecular agents at work, agents called proteins. Just as a symphony is the collective production of players in an orchestra, metabolism and growth of the cell is the sum of the actions of proteins. Proteins are the chemical catalysts, energy generators, motors, signaling agents, transporters, and even the underlying infrastructural units of the cell. Even the communication and cooperation between cells is accomplished by proteins. This sub-microscopic view of life gives new meaning to T.S. Eliot's proclamation that "[we] are the music while the music lasts." How proteins perform all these intricate tasks and how they are programmed to do so, are the foundational questions of biology. Although the study of protein function is itself a fascinating subject, here I will focus on how proteins are made in the first place.



The Basics of Protein Synthesis

Proteins are linear chains of amino acids connected by strong covalent bonds. Although there are only twenty different types of amino acids available to life, the sequence of amino acids in a protein of length N has 20^N potential possibilities. These possibilities allow for the exponential variability in sequence, which in turn is responsible for the variability of function among proteins. The particular sequence of a protein is encoded by a corresponding sequence of DNA. Our DNA therefore consists of the blueprints for all of the cellular machinery required for life. To synthesize a given protein, a mirror copy of the sequence of DNA corresponding to the protein is transcribed in the form of mRNA. The information from the mRNA is then translated into the protein sequence by tRNA, which maps every three letters of the mRNA to a unique amino acid on the growing protein chain (1). This sequence of amino acids that defines the protein is called the primary structure. The actual three dimensional structure of the protein is defined as its native fold. The fold is characterized by local repeating interactions, called secondary structure, and long-range interactions called tertiary structure. The fold is stabilized by a range of intra-protein interactions spanning the covalent disulfide bridge, hydrogen bonds, purely electrostatic interactions, and van der Waals forces. Hydrogen bonding with the protein's environment (usually water) is also a powerful force in the compaction and stabilization of proteins (2).

The Protein Folding Problem

Called the protein folding problem, the exact means by which the protein attains its native fold, is still unclear. The importance of this problem was greatly magnified by Anfinsen, who showed that proteins can attain their native folds in pure water without the aid of any cellular machinery (3). For a self-interacting chain, one would assume that the existence of a unique fold that is much more stable than all other possible folds is unlikely. However, because life requires proteins to be reproducibly made with reliable functionality, natural selection has led to the evolution of protein sequences with a single fold that is more stable than the entirety of all other possible folds. The fundamental physics of the folding mechanism are the self-interactions of a chain with twenty different possible types of constituents. As such, it seems that we should be able to predict protein structure solely from protein sequence using first principles. Such a theory would allow the design of protein sequences useful for medicine, nano-machinery, and materials science (1). For example, current chemotherapy drugs cannot be tailored to fit exactly to the markers of cancerous cells, leading to the drug's disruption of noncancerous cells in the body. With the ability to design protein drugs that specifically fold to fit, the efficacy of chemotherapy could be drastically increased without the onset of side effects (4).

The Amazing Life of Proteins

There are things that uniquely self-organize (e.g. water crystallizing into ice), as well as complicated things that are reproducibly made by external machinery (e.g. airplanes). There are even cases of complicated things that non-reproducibly self-organize (e.g. the weather). Proteins are singular because they are complicated structures that reproducibly self-organize. This engineering feat at the molecular level is the scaffolding that all biological complexity is built on. Despite this formidable feat of molecular self-assembly, there is still one more hurdle proteins must (and do) overcome in order to make life possible. This is the time paradox, noted in 1968 by Levinthal (5). Consider the case of a small protein with only 100 amino acids. Assume that there exists a single most stable fold for this protein. If each amino acid in the chain can be in one of two rotational orientations (an underestimate), then there would be 2¹⁰⁰ possible folds for the protein. Even if the protein could try each of those folds in a trillionth of a second (well beyond the chemical limit of diffusion for such molecules), it would take on average 20 billion years for the protein to find the most stable fold. Aside from the fact that this is longer than the estimated age of the universe, proteins actually fold in the timescale anywhere from a millionth of a second to a second. Proteins constitute a subset of all possible amino acid sequences that possess both a unique stable fold and a fast folding pathway. Clearly, in order to be fully folded and active on the timescale that they are needed in the cell, proteins cannot afford to randomly sample all possible folds.

What We Know So Far

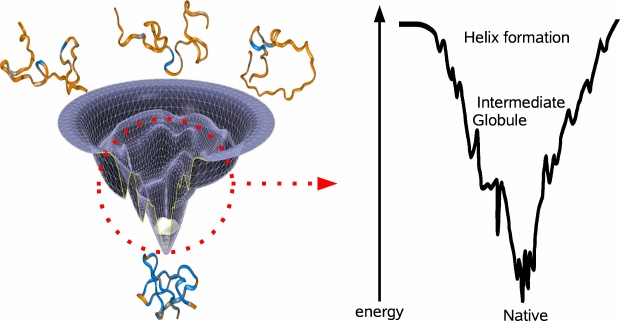
Suppose you tabulate all of the possible folds of a protein and imagine each fold as a unique coordinate on the x-y-plane. If you were to compute the energy of each fold and plot that on the z-axiz, then you would end up with the energy landscape of the protein (see figure). The lowest point of the energy landscape is the unique most stable fold. The general resolution to the Levinthal paradox was formulated by Wolynes and coworkers, who imagined the shape of the energy landscape as a funnel, evolutionarily biased towards the unique native fold. The specific conformations corresponding to the various parts of the landscape are not well understood and there is still debate concerning the fundamental steps proteins take to fold. The two prominent models involve either bottom-up or top-down folding. In the bottom-up model, smaller domains achieve stability and coalesce to form larger domains of stability. This perspective is attractive because folding occurs in parallel for all of the sub-levels, thereby quickly achieving the right overall fold. However, the extent to which domains can independently form may be limited in light of evidence that at the outset of the folding process, a protein can collapse into a ball with its water-favorable amino acids on the outside. Accordingly, the top-down model stipulates a fast hydrophobic collapse followed by slow local recombination.

There is evidence for both models of folding (6). For example, there is experimental evidence for microsecond timescale collapse into an intermediate globule, followed by much slower annealing to the final state. On the other hand, local independent formation of helix domains has been shown to occur even earlier in the folding process (7). Both processes seem to be crucial in funneling the protein towards the native fold (see figure).

The Future of Protein Folding

Due to the complexity and diverse interactions involved in the folding process, a new branch of computational and physics-based molecular biology has emerged in the past few decades. Some insights into the protein folding problem have come from explicit simulations of proteins in water. Such molecular dynamics simulations allow for the observation of numerous folding pathways and have already demonstrated remarkable accuracy in predicting native folds and folding times for rudimentary proteins (8). Insights from such simulations promise to increase alongside the exponential growth of computing power; we are nearing the time when atomic-resolution simulations can finally catch up with experiments in terms of spanning the entire folding time of proteins. When that day arrives, we will finally be able to watch the protein as it folds. Since cells were first visualized under a microscope, we have learned much of their inner workings. We may finally be on the cusp of understanding the folding and functioning of the players in the cellular orchestra.

References

1. H. Lodish, A. Berk, P. Matsudaira, C. A. Kaiser, M. Krieger, MP. Scott, S.L. Zipurksy, J. Darnell, Molecular Cell Biology 5th ed. (WH Freeman and Company, New York, 2004).

2. K. Huang, Lectures on Statistical Mechanics and Protein Folding (World Scientific, Singapore, 2005).

3. C. B. Anfinsen, Principles that govern the folding of protein chains. Science. 181, 223-230 (1973).

4. R. C. Jackson, Contribtuions of Protein Structure-Based Drug Design to Cancer Chemotherapy, Semin. Oncol. 24, 164-172 (1997).

5. C. Levinthal, Are there pathways for protein folding? J. Chim. Phys. Phys. Chim. Biol. 65, 44-45 (1968).

6. J.N. Onuchic, Z. Luthey-Schulten, P.G. Wolynes, Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 48, 545-600 (1997).

7. V. Daggett, A. Fersht, The present view of the mechanism of protein folding. Nature Rev. Mol. Cell Biol. 4, 497-502 (2003)

8. J.A. McCammon, B.R. Gelin, M. Karplus, Dynamics of folded proteins. Nature 267, 585 - 590 (1977)