It sometimes happens that my comments in the threads of my own blog get long and detailed (do not take this as me boasting about anything - it is just a fact). When that happens, I reason that they deserve to be promoted to a post by themselves, because threads are read by way fewer readers, and some of them might thus lose some interesting bit.

Because of the above I am (re)posting the text below, which explains some "a priori" reasons why quarks come with fractional electric charges in multiples of one third, why the sum of charges of fermions in one family nullify, and why our universe chose to have quarks of three colours. Beware, some non-trivial concepts of quantum field theory are needed, but I will try to make this as painless as possible (but not more).

Anomaly cancellation

If you take an electron, a neutrino, three up quarks, and three down quarks (you take three quarks of each kind because they come in three different colours, and quantum field theory sees as distinct entities, so you should too) you realize that the sum of their charges is zero. This is a convenient thing, but it is not by chance that it arises in our universe.

It is a thing called "anomaly cancellation" what forces the sum of charges of each fermion family to nullify. In general, the word "anomaly" has a different meaning in this blog, but I am an experimentalist after all. For a theorist, an anomaly is a loss of symmetry of a classical theory when the theory is quantized. It comes about from quantum effects that give a non-null contribution to the divergence of a conserved current.

Here I should open a long parenthesis where I would explain conserved currents, Noether's theorem, and the connections to the symmetry of a theory. I think there are better places where you may learn these things, so I just claim that it is not crucial that you fully understand these concepts to get to the bottom of this post and get a kick out of it.

If gauge currents -mediated by the photon, the W, and the Z- are anomalous we lose a property of the theory described by "Ward identities", and that is bad because upon Ward identities is based the renormalizability of the theory. A renormalizable theory is necessary to make sense of it and allow us to work out results; a non-renormalizable theory requires an infinite number of parameters, corresponding to arbitrary cut-offs we must impose on the momentum circulating in virtual loops of particles. It was 't Hooft who showed that local gauge theories are renormalizable, making them an instant hit for particle theorists at the start of the seventies.

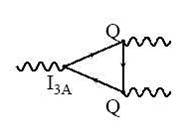So the standard model, the theory we all know and love, is only renormalizable if the triangular diagrams that couple an axial current to two vector currents cancel their contribution all together. An example of such diagrams is shown on the right, where an axial-vector current couples to the third component of weak isospin of the fermion in the triangular fermion loop from the left, and two vector currents couple to the electric charge of the fermion on the right. Note that if these diagrams cancel at lowest order, they will do so at every order and the theory remains renormalizable.

The beautiful cancellation of triangle anomaly comes about because we find that there is cancelation of these contributions family by family [where we are considering all fermions of a family as the combinations like (u,d,ν,e), (c,s,ν,μ), etcetera] if the triangle diagrams with one incoming axial current (which brings in a I_3,A factor of the fermion in the loop) and the two vector currents (which have two factors proportional to the fermion charges Q, since the amplitude of the photon-fermion coupling is proportional to the charge) overall cancel.
We need to have in other words: Σ [I_3,A * Q^2] = 0, where Σ denotes the sum over members of one family. With an electron, three up, and three down quarks, we find:

(I_3,A)_e * Q_e^2 + N_c * [ (I_3,A)_u * (Q_u)^2 + (I_3,A)_d * (Q_d)^2 ]

(where I hope symbols are understandable: N_c is the number of colours of quarks, I_3,A are the third component of weak isospins, and Q are the electric charges). This becomes:

 -1/2 * (-1)^2 + 3*[1/2*(2/3)^2 -1/2*(-1/3)^2] = 0.

So anomalies do cancel ! Also please note that if the up and down charges were f and 1-f, with f different from 2/3 (say in a different universe), the equality would be lost !

On the number of colours of QCD

Actually there is an even funnier circumstance concerning the above equation. If we take it but keep it generalized it by substituting N_c to the number "3" multiplying the square bracket above, we can couple that equation with the condition that Q_u - Q_d = 1, a condition which depends on the group structure of SU(2)xU(1), and which is independent on N_c. If we do that we find that

N_c = 1/(1+2Q_d)

which implies that if we want baryons with integer charge and three quarks, we are forced to choose an universe with quarks having fractional charge, and three colours!

If we chose instead N_c=1, we would get by force Q_d=0, Q_u=1, and there is no strong force with anti-screening, no antisymmetry of the colour part of the wavefunction. Hard to imagine such a world ! If, on the other hand, we were to pick N_c=2, we would get Q_d=-1/2, Q_u=1/2 and we do not have 3-quark states in our world.

I believe the above conditions do not "explain" the group structure of QCD and N_c=3, but they do indicate that such is the simplest condition to have baryonic matter in the universe. Interesting, ain't it ?