The Little Gauge that Could

This blog is a salvage job. I have towed my t-shirts with the GEM Lagrange density and field equations to the retraction dump, crashing global sales numbers. I have spent time picking through the rubble, trying to understand causes for the crash. While there are multiple reasons, I will focus exclusively on one issue: gauge symmetry.

The GEM proposal was based on a 4-vector potential. A 4-vector can be added, subtracted, or multiplied by a scalar. I then used the 4-vector in two distinct ways. One way employed the quaternion product rule (the group Q₈ over the real numbers) and was used to get the EM part of GEM. It was easy to spot how the division algebra of quaternions provided another means to write the same Lagrangian as seen in the traditional tensor approach. The other operation used on the 4-vector potential was the Klein 4-group (V or Z₂xZ₂ over the reals). That operation did not generate a valid new approach to gravity as I had hoped.

One can construct the fields of EM in potential form by taking a simple 4-derivative of the 4-vector potential using the quaternion product rule:

$vec \left[(\frac{\partial}{\partial t},\vec{\nabla}) \times (\phi, \vec{A}) \right] = \frac{\partial \vec{A}}{\partial t} + \vec{\nabla} \phi + \vec{\nabla} \times \vec{A}$

The fields written in potential form have the following gauge symmetry:

$\begin{align*} (\phi, \vec{A}) \rightarrow (\phi', \vec{A'}) &= (\phi, \vec{A}) - (\frac{\partial}{\partial t},-\vec{\nabla}) f \\ \\ vec \left[(\frac{\partial}{\partial t},\vec{\nabla}) \times (\phi', \vec{A'}) \right] &= \frac{\partial \vec{A}}{\partial t} + \frac{\partial}{\partial t} \vec{\nabla} f + \vec{\nabla} \phi - \vec{\nabla} \frac{\partial f}{\partial t} + \vec{\nabla} \times \vec{A} + \vec{\nabla} \times \vec{\nabla} f \\ &= \frac{\partial \vec{A}}{\partial t} + \vec{\nabla} \phi + \vec{\nabla} \times \vec{A} \end{align*}$

It is invariance under this gauge transformation in an action that leads to electric charge conservation.

Take a closer look a the vector identity that played a part in the preceding calculation, namely that the curl of the gradient of a scalar function is zero:

$\begin{align*} \vec{\nabla} \times \vec{\nabla} f &= \vec{\nabla} \times \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)\\ \\ &= \left( \frac{\partial}{\partial y} \frac{\partial f}{\partial z} - \frac{\partial}{\partial z} \frac{\partial f}{\partial y}, \frac{\partial}{\partial z} \frac{\partial f}{\partial x} - \frac{\partial}{\partial x} \frac{\partial f}{\partial z}, \frac{\partial}{\partial x} \frac{\partial f}{\partial y} - \frac{\partial}{\partial y} \frac{\partial f}{\partial x} \right) \\ \\ &= (0, 0, 0) \end{align*}$

It is essential to use the same scalar function throughout. The antisymmetry of the curl is the source of the cancellations.

I failed to find a legal variation on the EM work in using the Klein 4-group for the product instead of the quaternion product rule. One of the many problems such an effort faced concerns finding a gauge field and thus when put in an action, a conserved charge associated with the gauge symmetry. Look at the gradient of a scalar function using a symmetric curl symbolized by the boxtimes and having no minus signs, but putting the terms in the same spot as a curl:

$\begin{align*} \vec{\nabla} \boxtimes \vec{\nabla} f &= \vec{\nabla} \boxtimes \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)\\ \\ &= \left( \frac{\partial}{\partial y} \frac{\partial f}{\partial z} + \frac{\partial}{\partial z} \frac{\partial f}{\partial y}, \frac{\partial}{\partial z} \frac{\partial f}{\partial x} + \frac{\partial}{\partial x} \frac{\partial f}{\partial z}, \frac{\partial}{\partial x} \frac{\partial f}{\partial y} + \frac{\partial}{\partial y} \frac{\partial f}{\partial x} \right) \\ \\ & \ne (0, 0, 0) \end{align*}$

I had a blog where I tried to develop a complicated scheme for using conjugates to knockout the right combinations of terms, but that effort did not prevail.

Why not try a smaller gauge field? The scalar field f used in the EM gauge field can vary as a function of all four terms in spacetime: t, x, y, and z. A smaller gauge field could depend on time and just one direction in space, but not the other two. Use the smaller gauge field in the above calculation:

$\begin{align*} \vec{\nabla} \boxtimes \vec{\nabla} f[t,x] &= \vec{\nabla} \boxtimes \left( \frac{\partial f}{\partial x}, 0, 0 \right)\\ \\ &= \left( 0, \frac{\partial}{\partial z} \frac{\partial f}{\partial x}, \frac{\partial}{\partial y} \frac{\partial f}{\partial x} \right) \\ \\ & = (0, 0, 0) \end{align*}$

Since all the terms are mixed derivatives, all of the derivatives of a small gauge field that depends on only one spatial dimension are zero.

I feel like the salvage operation was a success. This little gauge reveals a little algebraic truth. I can imagine putting it to use someday.

But what is really going on? I have mounted on a 24"x30" canvas version 4 of my pipe cleaner representations of the groups Z₁, Z₂, Z₄, Z₂xZ₂ and Q₈:

The symmetry that is good enough to do EM is in the upper right, the flat blue box. The quaternions I use are the super complicated cube! The G part of the GEM proposal used the tetrahedron on the lower left. Use only one spatial direction and you get Z₂ on the upper left. One might not think the cyclic group of order two is worth investigation, but I think I will give it a try.

Doug

Snarky Puzzle: Fill in as many arrows as you can.

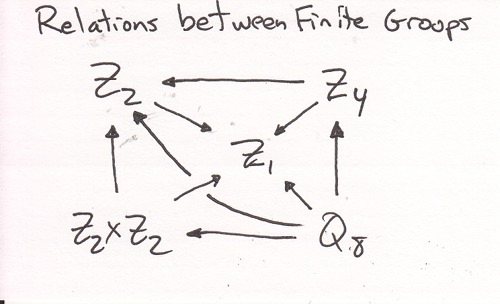
A few should be trivial, since the quotient group formed with the group itself is the trivial group. The vertical arrows could be a challenge unless you paid attention to this blog.

Google+ hangout: Saturday, 11AM

Next Monday/Tuesday: Riding the cyclic group

Related articles

Comments

Know Science And Want To Write?

Donate or Buy SWAG