I believe the experiment that proved the existence of a small effect of CP violation in weak interactions has been described in detail for large audiences a number of times, and I will not delve in its description here, save for remembering with a chuckle the story of the hypothesis of the transuranian fly. But before I do that I need to explain what I meant since the beginning here - the just as surprising phenomenon of the regeneration of the neutral kaons. Indeed, one cannot really describe the Cronin and Fitch experiment (no, I won't do it here!) without explaining in detail that marvelous quirk of quantum mechanical systems made of mixtures of states.
It so happens that neutral kaons come in two kinds: the proper K0 meson, which is made of a down and an anti-strange quark (d anti-s), and its antiparticle, the anti-K0, which is made of... Can you guess? A anti-down and a strange quark (s anti-d). These two particles are copiously produced by strong interactions e.g. when you collide an energetic proton with a fixed target, as was customary to do for breakfast in the fifties and sixties of the past century.
The K0 contains a strange quark, and because of that it is said to have a "Strangeness" of -1 (the minus sign has historical origins), and the anti-K0 has a Strangeness of +1. Strangeness was a property called in during the fifties to explain the funny observation that there existed particles (such as K mesons, but also others) that were copiously produced in the collisions of proton beams with nuclear matter, but took a long time to decay - that is, long with respect to what one would be able to compute, hypothesizing that the force that caused their decay was the same that caused their production. It was as if in a game of dice somebody rigged the game after the first roll, changing the dice from ones with six faces to ones with a million faces - good luck repeating the number you had thrown the first time then! [Hey, I am quite proud of the above analogy, but steal it if you wish. Just remember you heard it here first!]
The above was such a puzzle that physicists were led to invent the name strangeness to describe the property of those particles. Another observed fact, besides the asymmetric probability of production and decay of bodies containing Strangeness, was that they were produced in pairs: you could readily produce a pair of strange particles - but always one with strangeness and another one with anti-strangeness, as it was later figured out - but you basically never got to produce a single one.
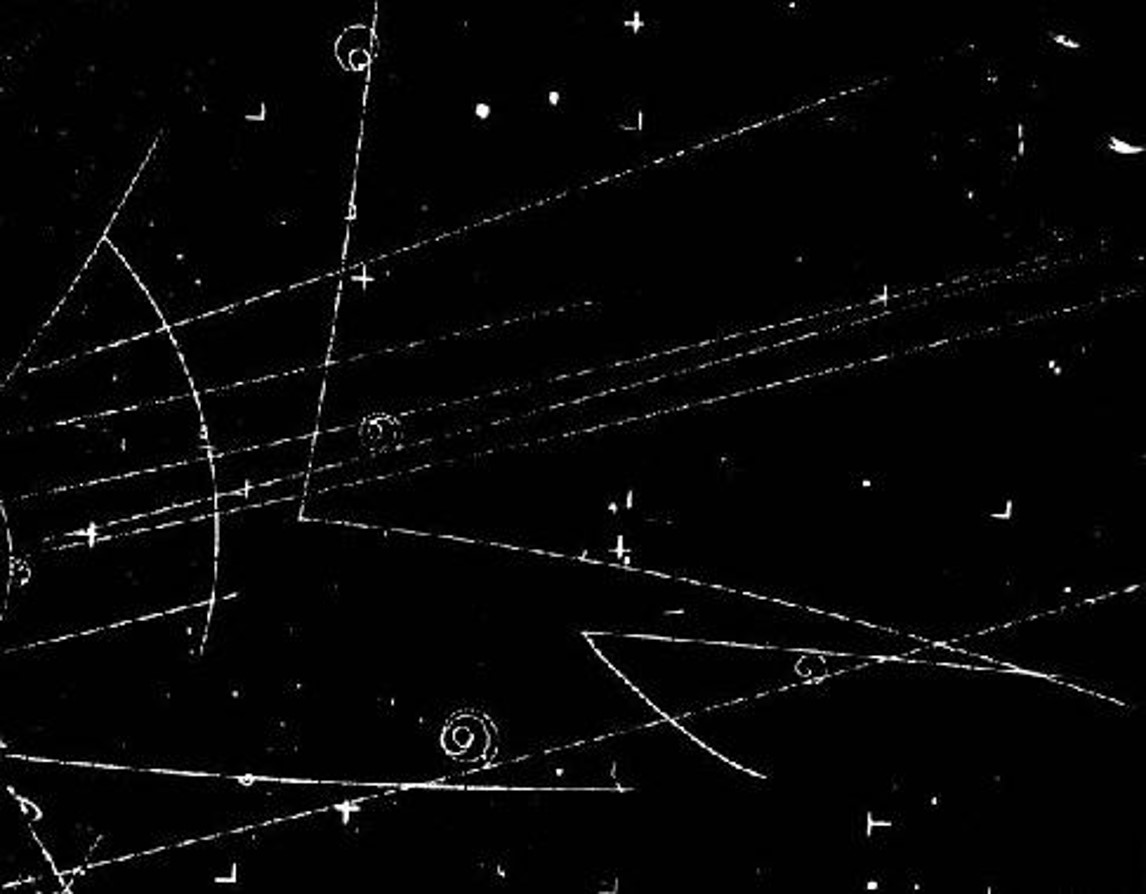
Above, two neutral strange particles (a S=+1 and a S=-1 particle, respectively a Lambda baryon and a K0 meson) are produced in a nuclear reaction by a pion beam entering the picture from the left, and soon decay into charged particle pairs (respectively, a proton and negative pion, and a positive/negative pion pair). The tracks are produced by ionization trails in a bubble chamber.
Strangeness was thus an additive property of physical systems: you computed the total strangeness S of a set of particles before some interaction as the sum of the strangeness of each. What was observed is that during the collision that created strange particles from non-strange ones this S number never changed - it was zero at the beginning, and it remained zero at the end of the collision, when a strange and an anti-strange particle pair was produced. Or one could smash a strange particle with a nucleus, and observe that the strangeness of the final state particles remained equal to the one of the initial particle.
But strangeness was violated in the decay of those funny strange particles: indeed, a neutral kaon could for instance decay to a pair of pions - lighter particles made up of light up and anti-down quarks (for example, in the case of the positively-charged pion).
It was only later understood that the production of strange particles involved the action of the strong nuclear force, which was unable to change the flavor of the quarks contained in the particles which took part in the reaction. The strong force was strong, and thus the reactions were highly probable - they occurred copiously, a sign that the interaction had a high probability of manifesting itself. But the decay of strange particles was mediated by the weak force, which was much less probable, and took a long time to transmute the strange quark inside strange particles into a lighter up quark.
Understanding quantum numbers and their conservation
In order to progress toward our goal of explaining the amazing phenomenon of K0 regeneration, we need to delve in their quantum-mechanical description. In quantum mechanics, a physical system can be called an eigenstate of an operator if the action of the operator on the state has the only effect of multiplying the eigenstate by a constant. If a particle is an eigenstate of the quantum operator that counts the number of strange quarks, it means it has a definite value of strangeness; e.g., plus or minus one as in the case of anti-K0 or K0 mesons. We write this as follows:
S | K0 > = - | K0 >
S | anti-K0 > = + | anti-K0 >
If I have a system made of a K0 and an anti-K0, strong interactions will be unable to change the total strangeness, because strangeness is a good quantum number for strong interactions: they conserve it. But weak interactions may instead change the strangeness of particles, so that for weak interactions the S quantum number is not conserved.
Another property of particles is called Parity, which is a multiplicative rather than an additive quantum number: systems either have parity of +1 and -1, and it is the product of the parity of the various pieces (modulo some angular momentum change, sorry for the detail) what defines the parity of the compound. It would lead us astray to describe the amazing properties of the weak interaction with respect to that symmetry operation (the combination of a mirror reflection and a rotation by an axis orthogonal to the mirror) - suffices to say that already in 1960 it was demonstrated in a glorious experiment that the weak interaction does not conserve the parity quantum number. I.e., if a system is an eigenstate of the parity operator (and the particles we are discussin here are indeed eigenstates of Parity, as they have a definite parity, +1 or -1), then the action of weak interactions on it may change their parity.
Weak interactions are really weird, aren't they? They violate the strangeness and the parity of quantum systems. And there's a third quantum number they violate: Charge conjugation. Charge conjugation (C) is another multiplicative quantum number, that distinguishes particles from antiparticles. Eigenstates of C parity are neutral states, and they can get a C quantum number of +1 or -1. For example, the photon has negative C parity, while the neutral pion has positive C parity. Being a multiplicative quantum number, the C-parity-conserving electromagnetic interaction allows the decay of the positive C parity neutral pion into two photons, which have collectively also C=+1.
Now, despite the insisting property of weak interaction of violating every rule we give to quantum systems, they were observed until 1964 to conserve the CP quantum number: the product of their C and P parity. If, i.e., you had a particle or system in a CP = +1 state, then weak interactions would respect that and no matter what they did (decay particles in the system, or make them react) they would leave the system's CP alone. In fact, physicists were pretty damn sure that CP was a quantum number that nobody violated. But then came Cronin and Fitch...
It's a K0. No, wait, it's an anti-K0. Jo, but wait...
Because strong interaction conserve strangeness, in a strong reaction that produces, e.g., a K0 - anti-K0 pair it does make a lot of sense to say that we have produced a pair of these bodies, which we identify as eigenstates of Strangeness (with S number -1 and +1, respectively). But because weak interactions violate S, it is better to describe these states as mixtures of eigenstates of the CP operator. Why mixtures? Because K0 mesons were observed to behave as a superposition of two neutral mesons with different CP properties: the K0_1 and the K0_2. The K0_1 decayed relatively fast into pairs of charged pions (pi+ pi-), while the K0_2 took a much longer time and decayed into a trio of pions (e.g., pi+pi-pi0). The original K0 and anti-K0, that is, were not eigenstates of CP, but a mixture of the two CP states. We can write them as follows:
| K0 > = 1/sqrt(2) [ | K0_1 > + | K0_2> ]
| anti-K0 > = 1/sqrt(2) [ | K0_1 > - | K0_2 > ]
and we can conversely write the two CP-eigenstates as
| K0_1 > = 1/sqrt(2) [ | K0 > - | anti-K0 > ]
| K0_2 > = 1/sqrt(2) [ | K0 > + | anti-K0 > ]
No problem for CP if a part of the original K0 decayed into a CP +1 state (two pions) early on, and then into a CP -1 state (three pions) later: not being created as eigenstates of the CP operator, they could do that. Indeed, they were a mixture of the two CP states. This produced the funny situation that if you started off with a beam of pure K0 particles (e.g. produced by some decay chain that generated them in a strangeness eigenstate -1), over time the K0_1 component would disappear more quickly than the K0_2 part, so that in terms of strangeness the beam could be interpreted as containing a part of anti-K0 mesons, because of the way you can write the linear combination of quantum states above!
The weak interaction processes that pull this trick off are called "box diagrams", where you may interpret the states as eigenstates of the strangeness operator, and you can track the strangeness in the particles:
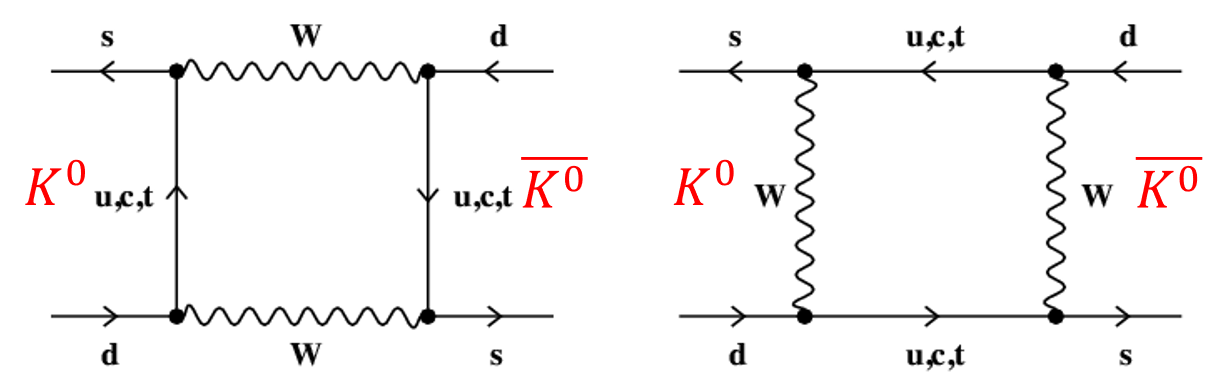
As you see in the diagrams above, which you should read left to right, with time running that way, a K0 (which contains an anti-strange quark, which in the diagrams are a line with an arrow pointing "backwards" in time) can be transformed by a "second-order" weak interaction into its antimatter particle, in two different ways.
The above phenomenon is called "strangeness oscillation": while progressively decaying, a beam of pure K0 particles will develop an anti-K0 component. As also the anti-K0 can do the exact thing and transform back into a K0, what we can observe is that the two component slowly become equal. In terms of the K0_1 and K0_2 CP eigenstates we discussed above, this means that the beam is now a pure K0_2 one, of CP -1, which slowly decays into three-pion final states. Aha. So is that it?
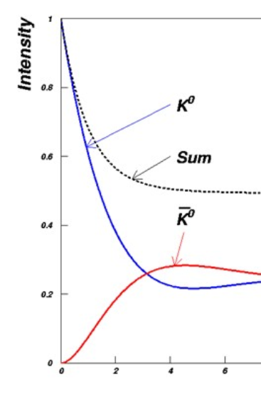
Above, a pure K0 beam will start a dance with its antiparticle, creating the phenomenon called "K0 oscillation".
No, it is not exactly all here. For those K0_2 that remain in the beam might pull off one further astounding trick if you let them traverse some nuclear matter. When they hit nuclei, the K0_2 particles will interact again by the strong force (which is much more probable than the weak interaction, as I already said). And the strong force cares about strangeness, so it will "see" the different strangeness components in the K0_2 beam. Now the strangest thing happens: nuclei are more keen of interacting with the strange quark in the anti-K0 than with the anti-strange quark in the K0, so they "eat out" a larger share of anti-K0's. When the leftover particles emerge, they have a larger K0 component, and this means that the beam can be interpreted as containing again a short-lived K0_1 fraction! In fact, we observe again two-pion decays, which had long stopped occurring.

The phenomenon of "regeneration" of the short-lived K0_1 component is a marvel of quantum mechanics, and it is at the core of the calculations that Cronin and Fitch had to do on the classic "back of the envelope" when somebody asked them about the transuranian fly. Without having to tell you about the whole CP violation experiment, which deserves another post, Cronin and Fitch had in their experimental setup a large helium bag vessel where a beam of pure K0_2 was injected, after having carefully let the short-lived K0_1 component die out. Helium is a light gas, so the regeneration of K0_1 was thus kept at a minium in the large gas vessel.
The objection that some physicists moved to Cronin and Fitch -who had proven that some of those K0_2 still decayed to two pions, thereby violating their CP quantum number, was that maybe there was some residual high-density material in the bag, which caused some K0_1 to regenerate thanks to nuclear interactions of the K0_2. The hypothesis was that a fly could have entered the vessel and provided the necessary amount of nuclei. A quick calculation showed that the density the fly had to have in order to produce the necessary amount of K0_1 regeneration, thereby explaining away the observed CP violating decays to two pions, was well beyond that of Uranium. That settled the matter!
The two physicists received the Nobel Prize in Physics for their CP violation experiment in 1980. But as I said, that is another story!



Comments