Anyway, in some way this rather startling concept applies to every man except researchers in fundamental physics - both male and female, in fact. There, all of us love our Standard Model - it is a theory so wonderful and deep, and so beautifully confirmed by countless experiments, that it wins you over forever once you reach enough understanding of its intricacies. And physicists have tried, unsuccessfully, to kill the Standard Model for over fifty years now.
Anomaly! Anomaly!
There will be others, but the latest attempt at making the Standard Model crumble and fall has been the relentless siege on a very subtle effect arising in the dynamics of the spin of the muon - an anomaly. Anomalies in our real world arise a bit everywhere - from temperatures of the oceans, to orbits of satellites, to US candidates to the presidency. I think I know something about the topic, as I went as far as to write a book titled exactly that way ("Anomaly!" - see at the bottom of this post).
However, in physics anomalies have a very special meaning: they are differences in the behavior of a quantum system from the expectation obtained by applying classical laws. Specifically, if you consider the classical description of a system that exhibits some symmetry, and quantize the system - by considering now the quantum-mechanical rules that govern its behavior - you may find out that the symmetry property did not survive the quantization procedure.
If the above does not ring a bell, worry not; it is not strictly necessary to understand such a cryptic concept in order to follow me down this piece. Let us rather consider the muon, a heavy brother of the electron that has a lifetime of only 2.2 microseconds. We can study the electromagnetic properties of muons and we find that there is a quantity we may define and measure, called the gyromagnetic ratio, which in classical electromagnetism should have a neat value, a submultiple of a well-known constant, but when you go out and compute it by taking into account all quantum phenomena that arise in the propagation of muons in an electromagnetic field, you find that the neat relationship is broken -there is an anomaly.
It is a tiny effect, to be sure; but it is one that can be predicted with astounding accuracy by applying the laws of the Standard Model to the muon. And what is even more amazing is that we can measure the quantity with a similar level of precision. What we are talking about is an extremely precise test of the Standard Model theory.
What makes the whole business even more exciting is the fact that there are potentially clean explanations of why a difference between theoretical prediction of the anomaly and observed value could arise, and they involve the existence of new heavy elementary particles, ones that we could discover with a more powerful version of the LHC. These massive particles would participate in "quantum loops" that arise in the interaction of the muon with the electromagnetic field, making themselves felt at a tiny but sizable level.
So you well understand why for the past two decades, physicists have been puzzling over the discrepancy between prediction and measurement of the muon anomaly. The discrepancy was at a level of three standard deviations for quite some time, but recently a very precise new experiment at Fermilab pushed the experimental accuracy further, exposing a striking 5-sigma difference. New physics? Is the Standard Model dead at last? Are there indeed new massive particles in those quantum loops?
Not so fast. The problem of the Standard Model is that, as precise as it is, it requires volumes of complicated calculations if you want to extract precision estimates of observable physical quantities. The reason is that these quantum loops can be nested into one another, in an ad-infinitum regression. What theorists do is to compute the effect of one quantum loop, then two, then add a third, and so on. But every time you consider one more loop, the number of new calculations you have to consider grows exponentially. The series of contributions to the quantity you are estimating is convergent, so even if you stop at the one-loop level you have a reasonable result; but if you need more accuracy, it's going to be time spent at the blackboard.
What will you be doing at the blackboard is to draw all possible combination of loops of virtual particles that can attach to the muon and photon in a graph that at leading order looks like this:
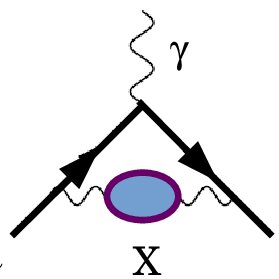
[Above: a Feynman diagram of the muon-gamma vertex.]
The black arrow is the muon, here shown emitting a photon toward the top. While it is at it, the muon can emit another photon which generates a loop marked with an X at the bottom, before the photon is re-absorbed by the outgoing muon. It is a bit like a juggling act what is depicted, and a subtle one. In X we may have an electron-positron pair being created and then re-annihilated; or in truth any other charged particle (all charged particles "couple" to the photon and therefore can participate in this electromagnetic trick).
But wait, it ain't over, as what I have described above is the calculation of electromagnetic forces on the muon. Yet a photon that is emitted by the muon (to let the muon "feel" the electromagnetic field it is moving in) can fluctuate into quark-antiquark pairs. And those annoying quarks may exchange also strong interactions among each other while they exist; and such processes cannot be calculated by series expansion, as with strong interactions a nasty thing happens: every time you increase the number of quantum loops the result bounces around - it is not a convergent series!
The trouble of the so-called "hadronic vertex" is all there: we cannot compute it exactly. Yet over the years we have devised devilish are approximation methods that bring us back into the game. And the final result is something like what is shown in the graph below.
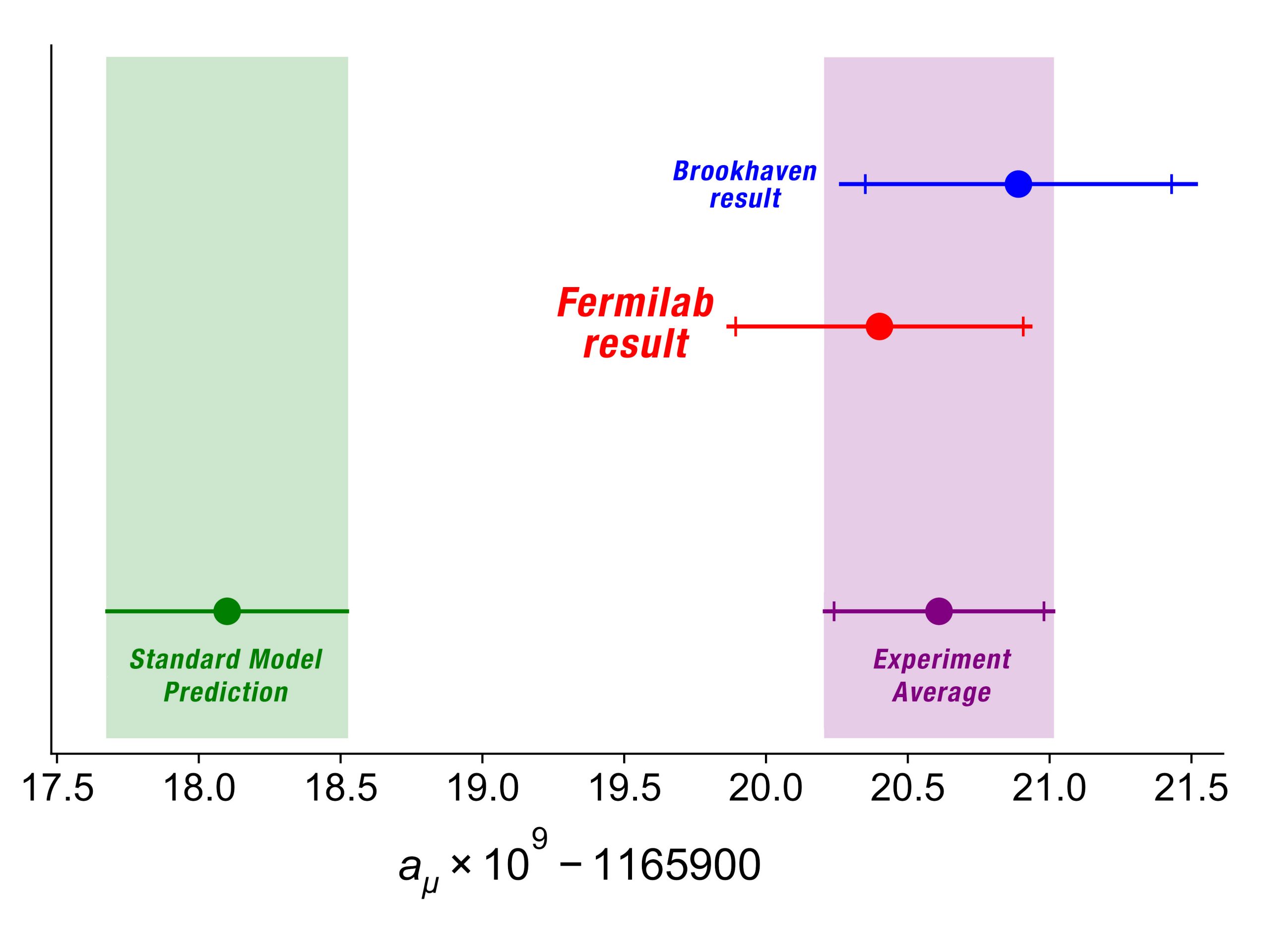
[Above, a comparison of theory and experiment (the graph is not the latest result by the Fermilab collaboration, but it serves the purpose of illustrating the discrepancy).]
There is a lot to unpack here, so let me try to explain. The theoretical prediction is the one on the left. It says what the muon anomaly should be measured at. On the right is instead shown the experimental result by the Fermilab experiment, along with an earlier result from Brookhaven. Once combined they make the purple bar. The purple and green bar describe two values that differ at a statistical significance level that calls into question systematic effects: it cannot be ascribed to a statistical fluctuation.
Here we should note that the precision of the theoretical estimate shown above is dominated by the approximated calculation of the hadronic vertex. The uncertainty on that contribution is also estimated - it could be larger. And if it were larger, maybe the tension between theory and experiment would soften...
Enter lattice calculations
Now, if all that there is to know about this effect was what I told you until now, you could be wondering why I started this article by saying that physicists are not killing the thing they love. In fact, there is another thing. There is another kind of approach to calculate the hadronic vertex in the muon anomaly, which relies on calculations "thrown on the lattice". What this means is that you can discretize spacetime and compute physical systems as if they only existed in a grid of points, with a tiny spacing that you can mathematically shrink to zero to reconcile with reality. The advantage of throwing a calculation on the lattice is that you can compute things you can't otherwise compute, like strong interactions among quarks.
Lattice calculations are only possible with enormous computing power. But that is something we now have. So a group of theorists has been working hard to compute the muon anomaly on the lattice, this time using a finer grid of points, which approximates the continuum much better than earlier. And guess what is the result: the calculation makes the Standard Model prediction agree with the experimental measurement at a level of less than one standard deviation!
The graph below shows a breakdown of uncertainties in the calculation made by the group, separately for 2017 (blue bars), 2020 (green bars), and their newly released result (red bars). As you can see, the uncertainties were shrunk quite significantly in the span of seven years.
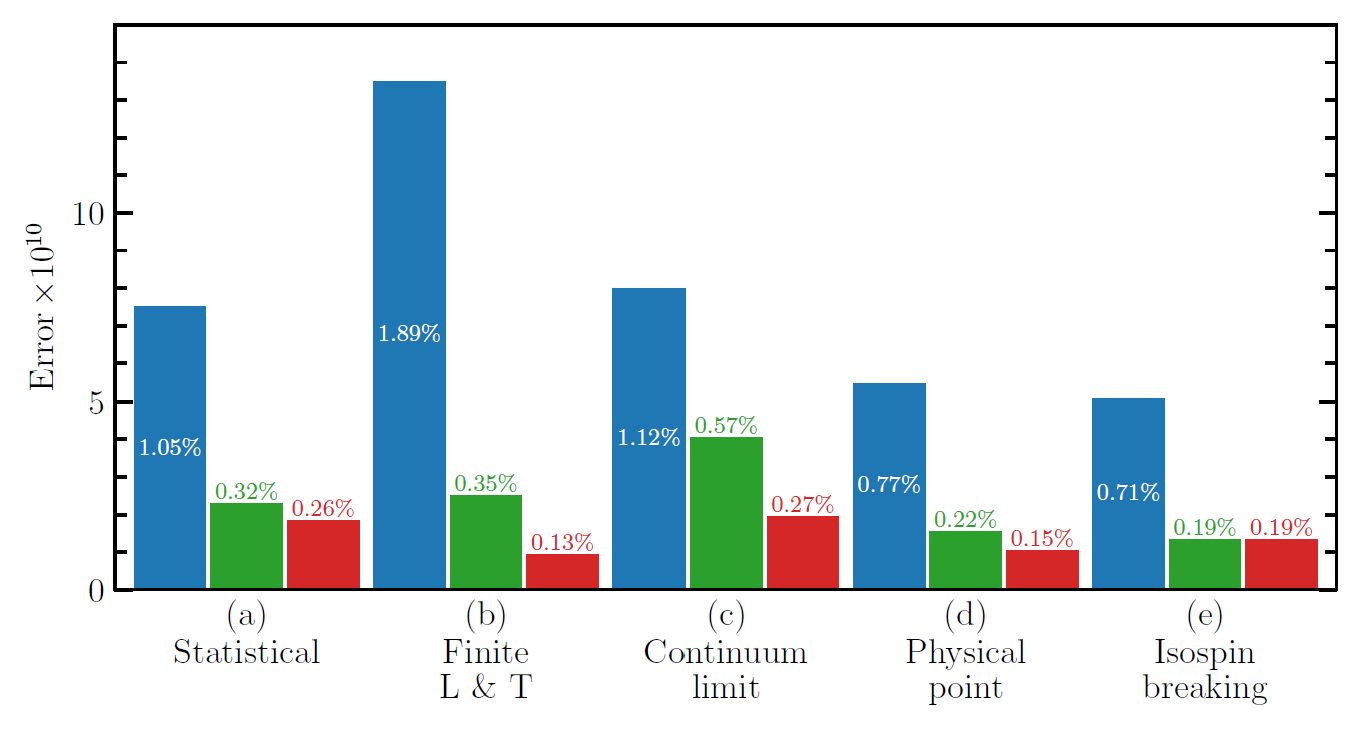
[Above: a breakdown of uncertainties from lattice QCD calculations of the muon anomaly, for the 2017, 2020, and 2024 results of Boccaletti et al.]
In this other even busier graph you can see the muon anomaly measurement (green bars at the top, and green band on the right) compared to various theoretical predictions. In red is the latest lattice QCD result. What is indicated as "white paper" (the blue band on the left) is the state of the art theoretical prediction not based on lattice QCD. Making reference to that result, which is believed to be correct by a good part of the community, forces you to conclude that there is a 5.2 standard deviation discrepancy with the experimental determination. However, if you believe in the lattice QCD calculation (red bar), the story is quite different!
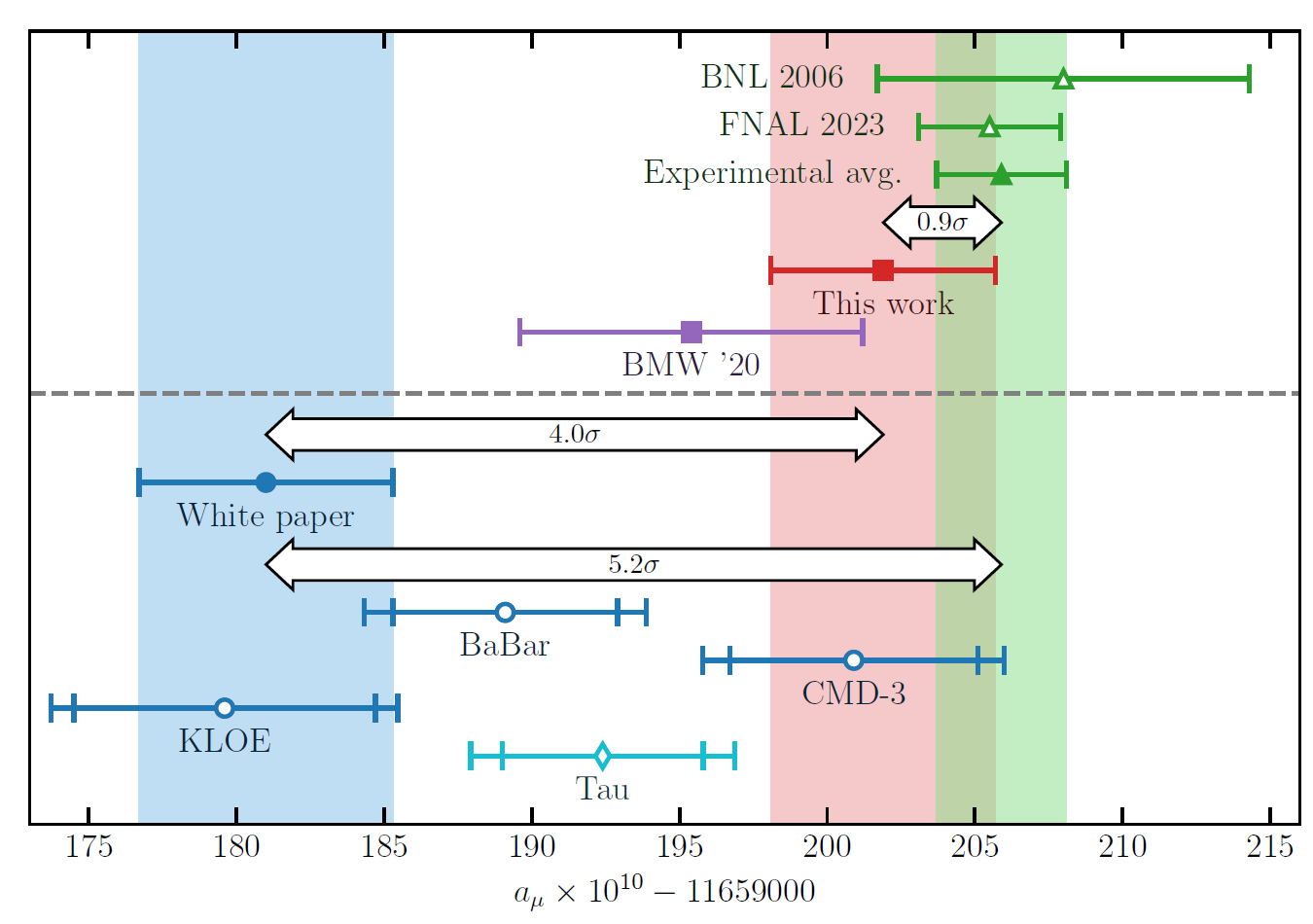
[Above: a comparison of various theoretical calculations and the experimental average of the muon anomaly. See the text for detail.]
So, do you take the red pill or the blue pill? You see, it would be great if the blue "white paper" result were correct - we would have basically killed the Standard Model and we would have all the reasons in the world for believing there are new heavy particles out there to discover. But in the presence of an independent result that uses a completely different calculation method, which is in great statistical agreement with the observation, we have to pause. From a Bayesian standpoint we have no choice but strongly suspecting that the white paper is off for some reason, and that the Standard Model is correct and Lattice QCD right on the money. This is because we trust the Standard Model enormously - it was confirmed in so many different ways, we cannot dispose of it just yet.
It will take time to understand whether the white paper result suffers from another wrong minus sign in a calculation of some obscure quantum correction (as it has happened already in the past) or if there is something intrinsically wrong in pushing the relative calculation to these levels of accuracy. But to me, the matter is becoming already a bit boring - nothing to see here, walk away!
---
Tommaso Dorigo is an experimental particle physicist, who works for the INFN at the University of Padova, and collaborates with the CMS and the SWGO experiments. He is the president of the USERN organization ), the coordinator of the MODE collaboration , and an editor of the Elsevier journals "Reviews in Physics" and "Physics Open". In 2016 he published the book "Anomaly! Collider physics and the quest for new phenomena at Fermilab".





Comments