The muon is a remarkable particle, and its characteristics continue to be of interest eighty years after its discovery despite the fact that we have measured them better than almost anything else around. So, for instance, the muon lifetime is known to better accuracy than that of any other unstable particle; and the muon anomalous magnetic moment remains at the top of our list of things to determine more precisely nowadays.

Why do we obsess on measuring to the tenth decimal place quantities that the Standard Model predicts with extreme accuracy ? Because the Standard Model predicts them with extreme accuracy, of course. Theoretical calculations can be matched to observations at a level of precision that would allow us to detect even tiny departures, and these would automatically imply that there is new physics not described by the model.

One interesting feature of the muon phenomenology is the way the particle decays. After an average lifetime of 2.2 microseconds the muon decays to an electron, an electron antineutrino, and a muon neutrino. The three light fermions are emitted preferentially in a configuration whereby the electron is kicked in one direction and the two neutrinos recoil in the opposite one.

(Picture from jick.net)

To explain the reason of the peculiar configuration note first of all that the muon spin, equal to 1/2 in h-bar units, must be balanced by those of the three final state particles. And all three final state leptons are quite light, so they are relativistic - meaning that their total energy is much larger than their rest mass. In such conditions, both the electron and the muon neutrino want to have their spin aligned opposite to their direction of motion - what is called "left-handedness", or also "negative helicity"; the electron antineutrino wants instead its spin aligned along its motion (right-handed, or positive helicity).

[Note that in the nice graph above it is a positive muon that is taken to decay, so the particles emitted are all antimatter copies of the ones I have been considering: a positive electron, which wants to be right-handed; and the two neutrinos which have swapped helicities with respect to what I have been discussing.]

The above constraints can not be satisfied if the neutrino and the antineutrino are emitted in opposite directions, for in that case the electron cannot be fully left-handed. The most probable situation is the one mentioned above: the electron goes in one direction, and the two neutrinos recoil in the opposite direction.

What that amounts to is that the electron tends to have a momentum which is balanced by the sum of momenta of the two neutrinos: so out of the 105 MeV of energy released by the decayed muon, the electron will likely get 50 MeV or so, and the two neutrinos will get 25 MeV each. All of this may seem obscure, but it is just relativistic kinematics coupled with the rules of weak interactions, plus the conservation of angular momentum and linear momentum.

Now, the momentum spectrum of the electron emitted by decayed muons can be measured with good accuracy, and its distribution compared to Standard Model predictions. The distribution indeed "peaks" at 52 MeV, above which value it drops like a stone (values above 52.5 MeV are forbidden by energy conservation). The distribution has been measured precisely and the comparison shows that the Standard Model indeed predicts the phenomenon quite accurately.

In a paper I found in the arxiv today there is a comparison of new theoretical calculations to the measurement of the momentum spectrum obtained from negative muons stopping in a heavy medium. While in vacuum negative and positive muons behave absolutely in the same way, in matter there is a difference. A negative muon can be captured by a heavy nucleus and start orbiting it like an electron does; while a positive muon cannot do the same as it is repelled by the nucleus due to its charge.

Muons orbiting nuclei cause a modification of the momentum spectrum of the electrons they emit when they decay. A detailed measurement of this spectrum is harder to perform than for free muons, and a comparison with theory is harder to produce as the theory requires more careful correction for radiative effects. In fact, in the past the TRIUMF collaboration had found a discrepancy between observed and predicted spectrum in this case.

In the paper it is shown that accounting for radiative corrections for muons orbiting nuclei, using a complex formalism whose description is beyond the scope of this post, allows to obtain good agreement between theory and experiment. This is shown in the figure below.



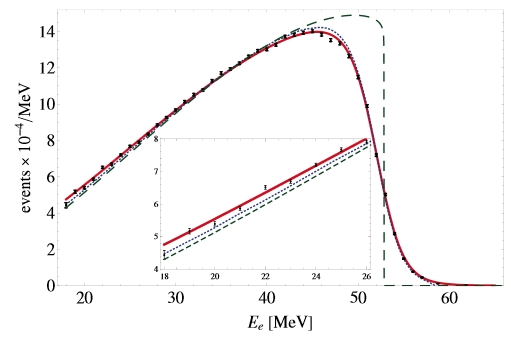
Here you can see the momentum distribution of the decayed electron, compared to several curves. The green curve is the one relative to non-captured muons, and is there only for reference; the other curves show the theory calculations with or without radiative corrections included in the calculation. You can see that the data agrees very well with the red line, which includes the corrections.

The interest of this result is twofold. First, the discrepancy between predicted and measured spectrum has been shown to be due to previously unaccounted quantum corrections: the Standard Model rulez. Second, one should not forget that these precise low-energy measurements have a bearing on the high-energy physics investigations, as for example the Higgs boson mass indirectly inferred from global fits to Standard Model observables do require those precise inputs.