One problem with the acceptance of dark energy and dark matter is that they are presented as if they are brothers, as if presenting merely the start of a new line of cheap ad hoc fudge factors: Dark energy, dark matter, dark force, what next? However, dark energy is not a fudge factor and not new.

Similar has been pointed out before, namely that dark energy is much less weird than usual pressure in Einstein’s general relativity:

The crazy point about dark energy is that something that pulls itself together expands, right? But that is not the contribution of dark energy. That part is usual general relativity. It has been accepted for almost a century: Pressure, although it pushes and "wants to expand", contributes to gravity, which pulls and leads to contraction.

Let me try a different way:

Take a usual pendulum, like a massive bob hanging from a string, and watch it swinging. Somebody writes down the equation that describes this pendulum: It has mass M and the length of the string L and also a term for the gravity of the earth for example. You can see how simple these formulas are at Wiki's Harmonic Oscillator. Now say that you see the swinging slowly damp down. No problem: There is a damping term D in the equation that describes that. Now somebody opens the window. The wind turbulences due to the window’s shape render the air flow around the pendulum somewhat periodic. You see the pendulum swinging more again – it accelerates. It accelerates just slightly and you yourself do not even feel the wind at all. Mysterious?

Of course not. And the equation that describes this is easily modified: Add an applied force term F(t). These terms in the equation of the harmonic oscillator, the damping D and the driving F(t), are completely natural. Especially, if you have another pendulum, say a vibrating string or a mass hanging from a spring, you apply the same or a very similar formula.

If you enter your observations of the oscillation, the formula will tell you whether there is damping going on: the damping D turns out to be non-zero. It also tells you whether there is a driving force that feeds the oscillation, namely if F(t) is non-zero.

You would be a fool to look at the data of a pendulum and start to reject physics just because the observations tell you that F(t) is non-zero. You might not yet know what exactly is driving the system, the wind or a magnet or whatever, but something pushes it.

Dark energy comes from the classical theory of relativity known for a century now. You have the usual equation and you look at a particular system to which the equation is applicable, the universe, and put your observational data, here from the observed expansion of space, into the formula. There is a driving term Λ (lambda) in there. Lambda was not put in there by hand much later. It should be in there, just like there should be a damping D and a driving F(t) in your equation if you want to describe an oscillator that you come across somewhere.

Here is Einstein’s equation G^uv + Λ g^uv = T^uv with the pressure-energy density tensor T on the right hand side and gravity, the G^uv, on the left side. Observation tells us that Λ is non-zero. This is called dark energy or, if it turns out to be constant over time, also cosmological constant.

Does dark energy exist? Does the driving term in the formula of the harmonic oscillator exist? It is right there on the paper where I wrote it down, and it would even exist if it turned out to be zero - but guess what, it is bigger than zero.

You may ask what the fundamental nature of dark energy is: Is it quantum, vacuum energy for example? There are many unknowns, but it is not valid to say that dark energy does not exist or has not been observed. Of course it is observed. It is the observed data that leave the dark energy term non-zero! And that is dark energy – the lambda term does have the units of energy – just like the pressure-energy density tensor T right next to it (g has no units).

Some do not "believe" in dark energy. Imagine I measure the damping term D of a pendulum to be non-zero and then people blabber about that "friction" cannot possibly be because what on earth is "friction" supposed to be.

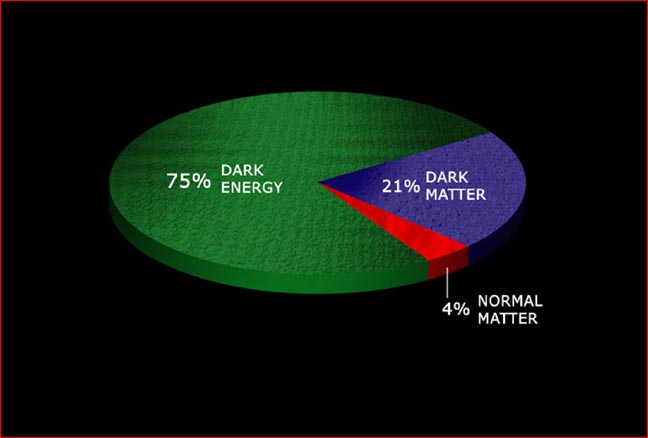
Everybody who throws dark energy and dark matter into one pot is highly suspect. Dark matter can be called a hypothesis, a good one by the way, although dark matter does not fit well to galaxy rotation curves – Modified Newtonian Dynamics (MOND) fits better (See: Begeman, Broeils, &Sanders 1991; Sellwood&McGaugh 2005). The driving term F in the formula describing an oscillator is not a hypothesis.