Ryskin's physics journey began with fluid dynamics, first in Russia, then in the US, at Caltech. Later, the flow of complex fluids, such as polymer solutions or liquid crystals. Then Brownian motion and Markov processes. In 2000, he became interested in geology and geophysics, particularly in the causes of mass extinctions and the origin of the Earth’s magnetic field. His current research is focused on cosmology. His academic home is Northwestern University, Department of Chemical and Biological Engineering.
The text below is Gregory's.
---
The vacuum energy problem arises because quantum fields fluctuate even at the absolute zero of
temperature, due to the uncertainty principle. These “zero-point” (T = 0) vacuum fluctuations
have non-zero energies. An attempt to calculate the vacuum energy density by summing up the
energies of zero-point fluctuations for all possible frequencies, leads to an infinite result. The
existing quantum field theory is not reliable for extremely high frequencies, so it seems sensible
to stop the summation at some cutoff value. However, with any reasonable cutoff, the result
remains ridiculously large, greater than an estimate based on astronomical observations by a
factor of order 10^55 or 10^123 . (Depending on the cutoff. The “rounded” number 10^120 is the one frequently quoted.) This has been called “the worst theoretical prediction in the history of
science”.
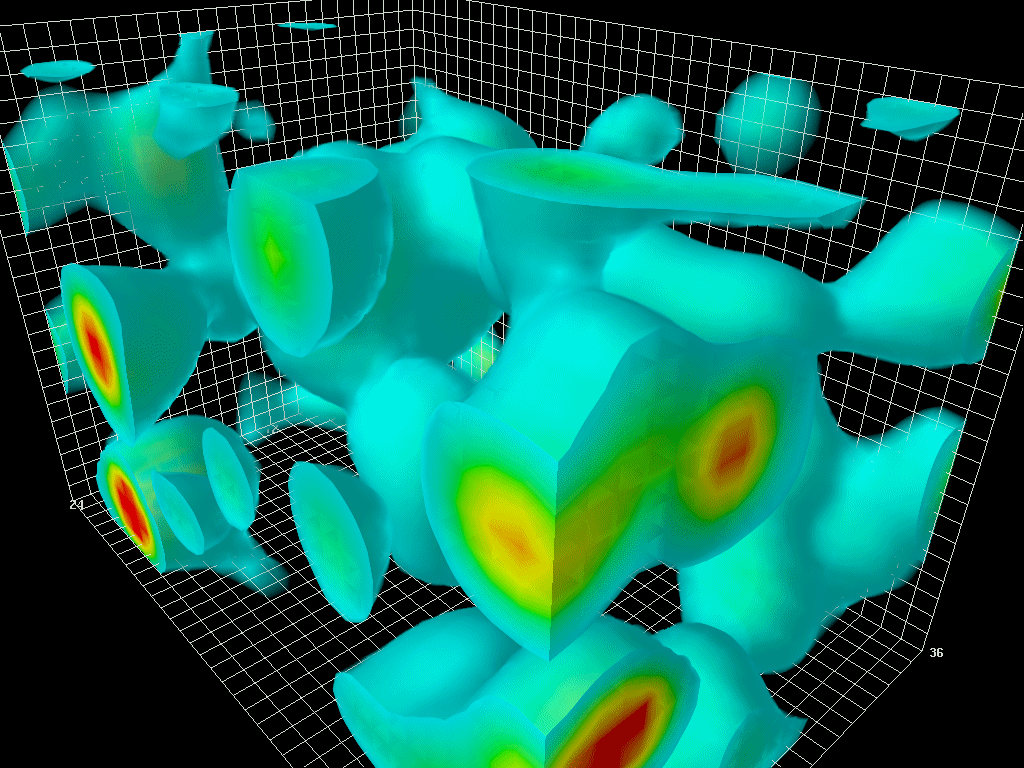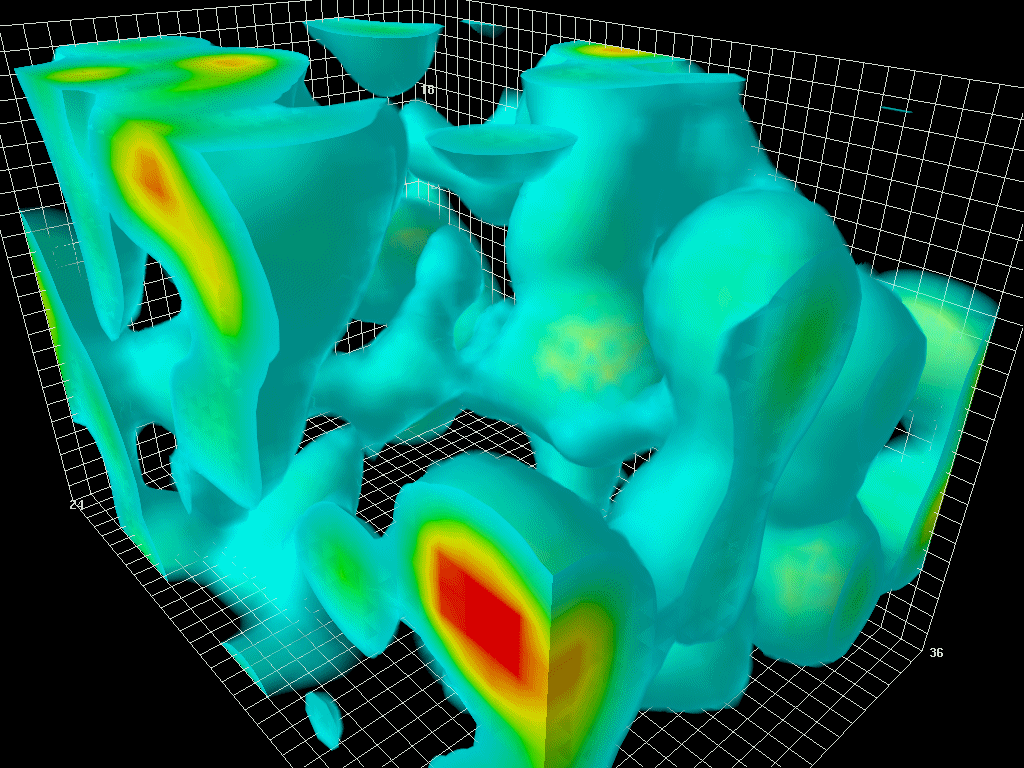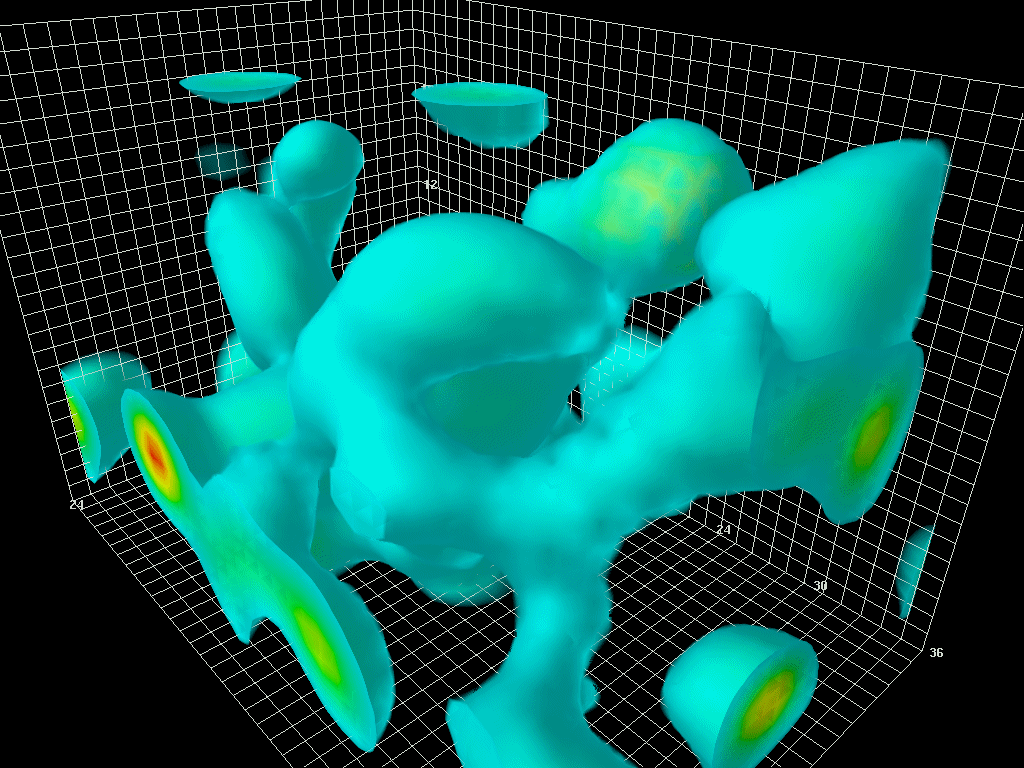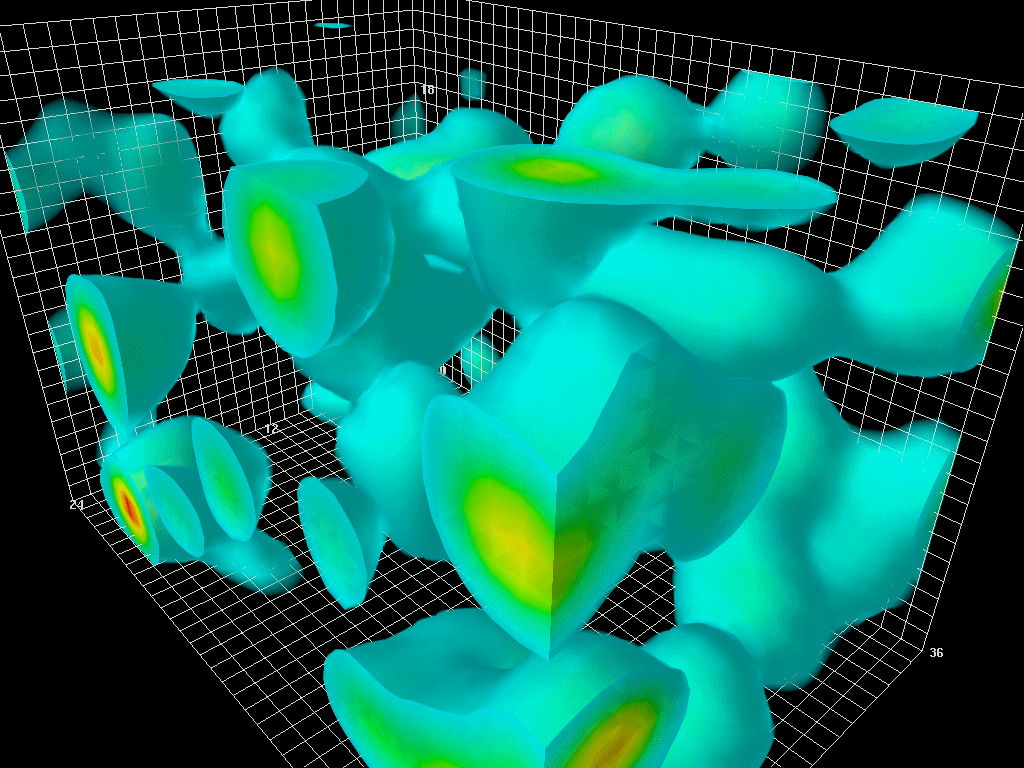
Figure 1. Zero-point vacuum fluctuations in the gluon field. (Gluons are massless force carriers,
comparable to photons. Photons carry the electromagnetic force. Gluons carry the strong
interaction force that binds quarks together to form protons and neutrons.) This animation was
produced by numerically simulating quantum chromodynamics – the quantum field theory of the
strong interaction – on a space-time lattice. The dimensions of the lattice box shown here, in
femtometers (1 fm = 10 -15 m), are 2.4×2.4×3.6. A box of this size could hold a couple of
protons; here it is empty, i.e., contains vacuum fluctuations only. For visual clarity, high-
frequency/short-distance fluctuations have been filtered out.
© Derek Leinweber, CSSM, University of Adelaide, Australia.
The problem has a long history. It was first discussed in 1916 by Walther Nernst, the father of
the third law of thermodynamics. Nernst considered zero-point fluctuations of the
electromagnetic field only. He concluded that “the amount of zero-point energy in the vacuum is
quite enormous”, but did not make a connection with Einstein’s general relativity. This was
done a few years later by Wolfgang Pauli, who found that, if vacuum energy were real, the radius
of the Einstein universe would “not even reach to the moon”. (In general relativity, all forms of
energy gravitate, i.e., induce space-time curvature.)
In his famous 1933 review of quantum mechanics, Pauli stated his belief that vacuum energy should be “unobservable in principle”. This did not stop others from trying to solve the vacuum energy problem. In the late 1940’s, Richard Feynman attempted a solution via a drastic reformulation of quantum field theory. His basic idea was simple: get rid of fields and consider particles only. For example, vacuum fluctuations can be viewed as momentarily existing virtual particles; more precisely, as virtual particle-antiparticle pairs (in order to conserve charge, etc.). Feynman hoped that without fluctuating fields, there would be no vacuum energy. His reformulation of quantum field theory was extremely successful and has been used ever since – but the vacuum energy problem
remained unsolved.
The vacuum energy problem is often identified with the cosmological constant problem. If
vacuum energy is non-zero, it contributes a source of gravity to the Einstein field equation of
general relativity. Such a contribution would be indistinguishable from that due to the second
free parameter in the Einstein equation – the cosmological constant. (The first one being
Newton’s gravitational constant.) The discovery that the expansion of the Universe is
accelerating, suggested that the vacuum energy density – or the cosmological constant – must be
non-zero. But, as mentioned above, the observations-based estimate is far exceeded by the
theoretical one.
My recent calculation ( https://doi.org/10.1016/j.astropartphys.2019.102387 Astroparticle
Physics 115, 102387, 2020), about two pages in length, combines Feynman’s original idea with
Gibbs’s “chemical” potentials, and shows that vacuum energy does vanish. Here is a brief
summary.
The virtual particle-antiparticle pairs certainly carry non-zero energy – on the microscale. But
the vacuum energy of interest in general relativity is a macroscale, thermodynamic quantity; its
value should be calculated using the methods of thermodynamics. Consider some volume of
vacuum. When a virtual pair appears in this volume viewed as a thermodynamic system, the
change in the energy of the system is not simply the bare energy of the newly added pair.
Instead, it is given by the so-called chemical potential, which includes also the total effect of the
interactions that the newly added pair has with all the other virtual pairs present in the system.
(The term “chemical potential” has become standard and cannot be replaced. This is unfortunate
because its literal meaning is misleading. Willard Gibbs, who introduced the concept, never
used the designation “chemical”. Chemical potentials are used in physics, in chemistry, in
materials science, etc.) A simple calculation, using the equations of thermodynamics, shows that
in vacuum, chemical potentials of virtual pairs are all equal to zero. Consequently, the vacuum
energy vanishes.
If this is so simple (in retrospect), why has not this been done before? Good question. Perhaps,
because chemical potentials play a crucial role? Consider this: the Bose-Einstein statistics was
published by Einstein in 1925; it applies to particles called bosons, of which photon is the prime
example. Its mathematical expression is a simple formula, which nowadays is written using
chemical potentials. Yet, the notion of the chemical potential of a photon did not appear in the
research literature until 1949 (!) (According to Google Scholar.)
If vacuum energy vanishes, what drives the accelerating expansion of the Universe? For my take
on this issue, see https://doi.org/10.1016/j.astropartphys.2014.10.003, Astroparticle
Physics 62, 258, 2015. This work demonstrates that the cosmic repulsion, responsible for the
acceleration, is an emergent property of general relativity applied to the Universe as a whole. Its
effect is observable on cosmological scales only.



Comments