While creating new springs to support a cephalopod-inspired imaging project, a group of Harvard researchers stumbled upon a surprising discovery: the hemihelix, a shape rarely seen in nature.
Helices are three-dimensional structures, like a corkscrew or a Slinky toy, and hemihelices form when the direction in which the spiral turns—known as the chirality—changes periodically along the length. The reversal in chirality is called a perversion.
Finding a hemihelix made the researchers wonder: Were the three-dimensional structures they observed randomly occurring, or are there specific factors that control their formation? The scientists answered that question by performing experiments in which they stretched, joined, and then released rubber strips. Knowing precisely how to make the structures, predictably and consistently, may enable scientists to mimic the geometrical features in new molecules that could lead to possible advances in modern nanodevices, including sensors, resonators, and electromagnetic wave absorbers.
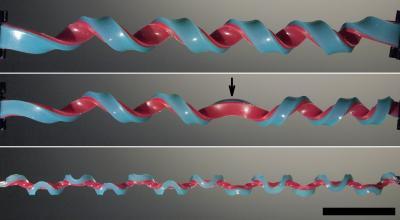
This is an illustration of a helix (top), a hemihelix with one perversion marked by an arrow (middle), and a hemihelix with multiple perversions (bottom). The scale bar is 5 cm for each image. Credit: Jiangshui Huang
"Once you are able to fabricate these complex shapes and control them, the next step will be to see if they have unusual properties; for example, to look at their effect on the propagation of light," says Katia Bertoldi, Associate Professor in Applied Mechanics at the Harvard School of Engineering and Applied Sciences (SEAS).
The shape that Bertoldi and colleagues at SEAS unexpectedly encountered is a hemihelix with multiple "perversions."
The team was trying to make two-dimensional springs by taking two strips of rubber material of different lengths and stretching the shorter one to reach the same length as the longer one and then sticking them together, explains David R. Clarke, Extended Tarr Family Professor of Materials at SEAS. "We expected that these strips of material would just bend—maybe into a scroll. But what we discovered is that when we did that experiment we got a hemihelix and that it has a chirality that changes, constantly alternating from one side to another."
Jia Liu, a graduate student in Bertoldi's group, tested differences in the aspect ratio—the width-to-height ratio of the rubber strips—and discovered that when a strip is very wide relative to its height, it produces a helix. Further measurements revealed that there is a critical value of the aspect ratio at which the resulting shape transitions from a helix to a hemihelix with periodic reversals of chirality.
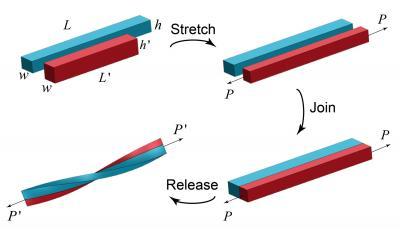
This image shows the sequence of operations that leads to the spontaneous creation of hemihelices and helices. Starting with two long elastomer strips of different lengths, the shorter one is stretched to the same length as the other. While the stretching force, P, is maintained, the two strips are joined side-by-side. Then, as the force is slowly released, the bi-strip twists and bends to create either a helix or a hemihelix. Credit: Jia Liu
Other classes of materials would simply break when stretched to the mismatched strains that the polymers endured—likely the reason this behavior had never been observed before.
"We see deterministic growth from a two-dimensional state—two strips bonded together—to a three-dimensional state," Liu says. "The actual number of perversions, the diameter, everything else about it is entirely prescribed. There is no randomness; it's fully deterministic. So if you make one hundred of these, they'll always perform exactly the same way."
Bertoldi adds: "From a mechanical point of view you can look at these as different springs with very different behavior. Some of them are very soft and then they stiffen up. Some are more linear. Simply by changing geometry, you can design this whole family of springs with very different behavior with predictable results."
Bertoldi and Clarke believe that their findings provide important clues for how to fabricate a variety of three-dimensional shapes from flat parts.
"Intellectually, it's interesting—and we believe it is significant too," Clarke says. "There are a variety of complex shapes in nature that arise as a result of different growth rates. We stumbled quite by accident on a way to achieve fully deterministic manufacture of some three-dimensional objects."




Comments