I have been again teaching two subjects where electric and magnetic phenomena are important (atomic physics and solid state physics) and met naturally new students. I always tell about the SI system and its history, but ask the students to use "for thinking" the Gaussian-like system (Carl Friedrich Gauss 1777 – 1855, portrait from Wikipedia) , where there is either a strength constant, or the units of charge are defined so that one gets the force as product of the two charges divided by distance. Potential, field energy density and all that are then simply expressed through the field strength, charge, etc, there is definitely no 
need for introducing "vacuum permittivity". In good textbooks and also on Wikipedia the students can learn that all this is simply connected with the choice of units, but now some of the students believe more in the existence of  "vacuum permittivity" - it is in the book. And the formulas look perhaps more impressive I like them as simple and logical as possible, some people actually prefer the fluffy form.
The advantage of Gaussian-like systems of units is  that the field strengths of the electric and magnetic fields have the same physical dimension, as required by special relativity, and this dimension is such that the field strength squared gives energy density, here we can perhaps try a formula

              

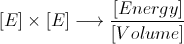
It further turns out that the field strength and the charge never appear "alone", always in sort of quadratic combination as in the formula above. In the modern language we simply define the strength of electromagnetic interaction through the so called fine structure constant, containing the charge squared - quadratic as I mentioned. In the modern theoretical physics we do not need any other charge than the elementary charge unit, so charge is just multiple of the elementary one, a number without dimension, just count. It all works beautifully in modern physics, so we do not talk about it much. In advanced courses we use "natural units" and replace everything by one (sort of). So the much older Gaussian system is in a way more modern than our international SI.

The reason for this now will come as a sort of theorem, which I have also seen expressed even in older writings. The problem with SI is descibed by its earlier name: rationalized MKSA, meter, kilogram, second, Ampere. The problem is with Ampere, fixing one extra unit. The old masters talked about three necessary fixed scale - for the length, time and mass. All the other phenomena are secondary. SI gives electromagnetism a special place, but through the "permitivity of vacuum", and these infamous four pi coming from the rationalization.

All this is well described, for example in the classical Classical Electrodynamics by J.D. Jackson, and by some historians. But what is not discussed, as far as I know, is this question: why do we need just three scales and not just two, or four like SI tries to convince us?