When we teach, and even communicate with people whom we assume to belong to some sort of common circle with ourselves, we simply assume that our audience knows or at least have heard about certain things.

For example, with people belonging in some sense to physics I would expect that my physics students would at least know about Bessel functions. I was wrong. One has heard the name, the others had not any idea. And they did not know practically how to plot functions on a computer. Two did know sort of, but only using "Origin". And so on. I do not want to complain. They are bright young people and they know lots of things, but not all what I - and most of my colleagues - would expect the students to know. 

And then you start looking into a virtual mirror, are there things people expect me to know - and I have no idea about them? Well, there must be. And one such thing is one aspect of the elliptic motion, a popular topic in all introductory physics courses.

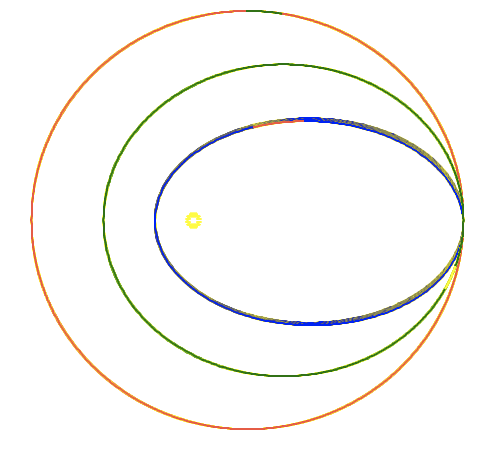
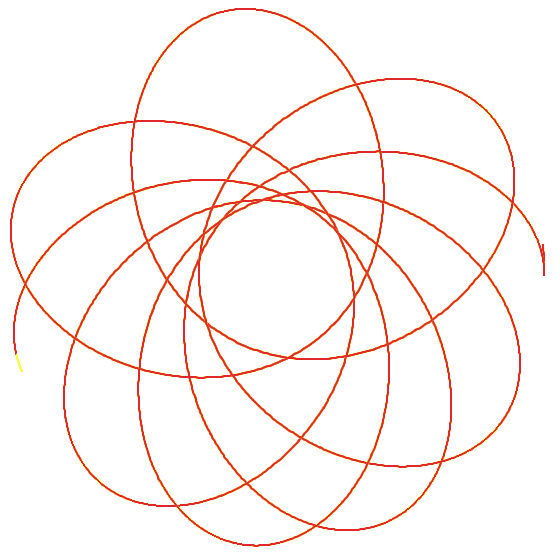
Yes, I know about the Kepler ellipses and all about Kepler problem as we teach it in introductory Classical Mechanics (see picture) , and I even know a lot about Runge-Lenz vector, because I in fact worked with related problems in atomic physics. But I assume that there is only this elliptic trajectory motion. My special knowledge even confused me, because it tells me that all the other potentials lead to unclosed trajectories (see picture, rosettes - in the picture the force is nearly as the inverse square of distance force field of gravitation, but with replacement of the distance by a slightly modified distance).


Here comes my own missing knowledge, before my "discovery" in simulations. There is a "force field" which leads to elliptic trajectory, in addition to Kepler ellipses. And many people know it, and they would probably expect me to know it.


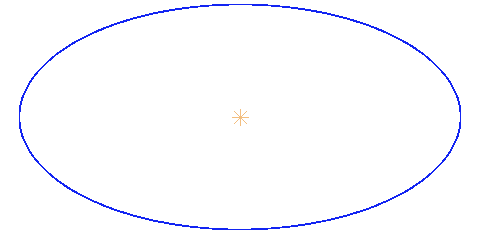
It is a different ellipse, however. While the Kepler ones have the centre of forces in the focus of the ellipse, this alternative one has the centre of forces in its own centre (see figure). Now, dear reader, would you guess what is that other force field? Do not rush to answer here, let other readers reflect on this question undisturbed. I will write one more little story about this in a few days - and then I would be glad to see many elliptic comments.