Theoretical Physics - it is cool. Especially elementary particle physics. Especially Quantum Field Theory. It uses renormalizations of constants, which is out of comprehension to most layman people. You know why? Because theorists first write their Lagrangian for, say, electrons and photons and later on declare it not to be for electrons and photons. So if you are a layman, you just suck at this moment.

They say - it was in fact written for "bare particles". You see, theorists know something experimentally unknown. Theorists say: in order to get the electron-photon Lagrangian we must carry out the fundamental constant renormalizations. Tricky is that QFT, but clever are the theorists!

Lagrangian meant by theorists for electrons and photons, but turned out not describing electrons and photons - it is not a theorists failure, according to some. Together with constant renormalizations it is their glory. They say so and we must believe them - it is the top of intellectual achievement of mankind ;-)

There is, however, a minority of people who see this situation as a failure. First it was QED fathers who expressed their worry about those renormalizations. The fathers knew better than anybody else what they were developing and what they arrived at. They were against renormalizations and for reformulation of our theories. Later on and with time, excellent students learned how to do renormalizations and started to practice them worldwide. You know, practitioners are much more numerous that theory developers. So the current situation is not in favor of those theory developers who are unsatisfied with self-fooling - the latter represent an extreme and chased minority today.

I myself belong to this minority. The truth is that theory developing (improving) is much more difficult task than theory applying. Especially when you go against a "consensus". You cannot even get elementary funds to carry out your research program, so you do it on your own. Yet, I have already something original to share (an article version is here or here).

I managed to remove the heaviness of QFT consideration and reduced the essence to a simple mechanical problem (a toy model). Any theoretical physics student can follow it. I show how we may misunderstand an experimental situation and how we may fall in error in describing it. The mechanical problem, however, is quite analogous to QED and CED because it was derived from there and made comprehensible to everybody.

A Toy Model

Let's suppose that acceleration of some macroscopic body excites some waves. To be closer to CED and QED, let's imagine we do not know how this body is built up in reality, but think it is simple. First we describe the body motion as a motion of a point-like particle (Newton equation). It works fine and we even advance a fundamental idea that our body is truly elementary and point-like (and we are then fundamental physicists).

Later on experimentalists discover waves created with the body acceleration. (For simplicity we consider only one frequency.) So they write down a phenomenological equation of a driven oscillator next to the Newton equation, both equations being experimentally justified:

The body mass , excitation efficiency 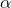, and frequency  are well defined in these equations and are phenomenological parameters. Nothing is bare here. The equations are coupled, but seemingly "not completely" - the oscillator "feels" the particle acceleration and the particle does not feel when it "pumps" oscillations.

Finally, we theorists decide to intervene and couple better these two equations - for the sake of energy conservation law, according to our fundamental notions. We think the energy transmitted to the oscillator is small and the losses were not that visible in experiments. So we want to preserve the driven oscillator equation and add some small "resistance" term into the mechanical equation. Indeed, without that "radiation reaction" the possible energy variations of our body are not related to the oscillator energy variations: . With this in mind, we advance an "interaction Lagrangian" or a "coupling term" that provides conservation of something, like in CED:

here is a self-action term containing the famous cut-off . New, coupled equations now read:

We see that the oscillator equation is the same as in (0) and the particle equation obtained a "radiation reaction" term, as we wanted. But our development surprisingly worsens agreement with experimental data! Indeed, the new equations are easily rewritten as (I multiply the oscillator equation by M_osc):

You see, the proper frequency (when F_ext = 0) is now different, the body reaction to an external force (acceleration) is different too, and the excitation efficiency (coupling) according to (3b) is different from that in (0). Our new equations became inadequate for describing the phenomena, even with finite "corrections".

Why is it so? Because the particle acceleration , from a known function of time in (0), became an unknown function and coupled to  in (3a) so we have changed in fact the oscillator equation contrary to our intentions. We may call it our mathematical error. Technically our coupling (interaction term) is of kinetic character and it modifies the mass terms involved in the original equations.

Remember, we just wanted to add some small "resistance" into the mechanical equation, but arrived at different dynamical systems (3b). It means we failed to couple correctly these equations. It means our understanding was wrong (the math was simple!). Time to revise our "fundamental" ideas and, of course, there is no reason to blame the Nature. This is what the fathers were talking about.

However another kunststück was indoctrinated. Having found no physical way to reformulate the theory, people started to keep to the wrongly coupled equations, and to restore the theory-experiment agreement people started practising the constant "renormalizations" in these equations. They discard those "corrections" to the fundamental constants (and the brackets in denominators are replaced with unity as if ) and, oh a miracle, the agreement with experiment is restored! Exactly renormalized equations of our toy model are the following:

They have good solutions corresponding to experimental data. The variables (equations) are coupled, but in a different way. You see, renormalizations are a "repair" or a "fix" of a badly coupled theory ("doctoring numbers" in solutions, according to P. Dirac). This was evident to QFT fathers but not to most modern theorists. Modern theorists say - there is no discarding but absorption of corrections by bare particle constants because the better coupled equations (3a) were written for "bare" particles with non-observable constants! Now tell me, my dear reader, do you find this "bare particle physics" convincing to you? I personally see cheating in such an "explanation".

Look at (3a) again. Terms proportional to alpha considered perturbatively give corrections to solutions even in absence of external forces. These corrections are interpreted as "physical phenomena" with "bare particle" like "vacuum polarization" that changes coupling, etc. Do not believe this, it is we who changed our equations, not physical phenomena with "bare" particles, let's not fool ourselves. To arrive at (4) we changed the equations twice: (0)->(3a) and (3b)->(4), that's it. In the most modern, Wilson's interpretation of renormalizations, to keep to (3) and to justify renormalizations they speak of a second-order phase transition! Of course, such a second-hand phase transition only happens during calculations and in heads of renormalizators, not in reality.

My example is exactly solvable and this permits to show that after renormalizations we return factually to the driven oscillator and Newton equations we started from. For a uniform external force from (4) we get our initial equations (0) about which we thought the energy was not conserved. Indeed, with a variable change we get:

, 

This system is equivalent to (0). However with this simple example we can now understand that the original equations were for the center of mass and for the relative (internal) motions. When the external force stop acting, the variable describes a free motion and describes free internal oscillations. In other words, the external force only acts on one of constituents of a compound system, transfers energy to its center of mass (global) motion and to its internal energy, both energy increments being additive. This is an important lesson. Even decoupled, the original equations (0) described well the physics, and the energy is already conserved in them if these equations understood correctly. It is evident from my toy model, but is still misunderstood by "elementary particle" theorists because all this is not visible in their perturbative approach. Now in (0)! we just rediscover complexity of our macroscopic body - it is not as "fundamental" and "elementary" as we are used to wrongly think of it. It's a "kammerton", a compound system. Here was our conceptual physical error. Who said our macroscopic body was "elementary"?

With the right insight we could have avoided those erroneous steps in theory development (0)->(3a) and (3b)->(4) and their "justifications". The average trajectory of permanently coupled body (at which we apply the force) <r_p> may practically coincide with the CM average trajectory <R> usually observed in experiments. In proceeding from (0) to (3) we mistook an average particle dynamics for a microscopic one.

By the way, without averaging the "particle" solution r_p = R + r_osc is "infrared-divergent" in a one-mode low-omega case because the frequency is in the denominator of the oscillator solution:

It just means a large amplitude of oscillations if the oscillator is weak ( ) which is physical.

You know now that we always deal experimentally with quasi-particles in compound systems rather than with "elementary" but "interacting" particles (I mean observed proper frequencies and measured total masses). In the frame of such understanding the "coupling" is potential rather than  kinetic so no mathematical and/or physical problems arise. Quasi-particle dynamics is free from unnecessary "corrections" to the fundamental constants and in QFT it represents equations for occupation numbers without mathematical difficulties. Good bye "interaction" of "non-interacting bare" particles in empty space!

I also show that renormalizations of constants done perturbatively, in spite they may work sometimes, do not reveal the right physics of coupling. Finally, I explain why renormalizations - violent modification of some terms - accidentally work in our example. It is due to simplicity of some models when one may be just lucky. More complicated "our theories" constructed by analogy with "successful" cases are non-renormalizable due to lack of luck and not because of "unknown phenomena" at short distances.

I hope my presentation will be interesting for people who care.