In this third part I want to examine in some detail a few additional specific factors that have the power of creating the conditions of false discoveries in fundamental physics: Background mismodeling, A Posterioriness, and (involuntary or else) data manipulation. I will leave the conclusions to a fourth part of this article.
Background Mismodeling
Loosely connected to the look-elsewhere effect is the issue I will call "Background Mismodeling".
It often happens that while studying a dataset for some measurement, an experimentalist will produce many histograms to control e.g. how well the simulation of backgrounds models the kinematical distributions of the data (this is also sometimes called "Monte Carlo validation"). The experimentalist may thus occasionally encounter a region of phase space (i.e. a particular configuration of the kinematics of the observed particles) where there is a significant difference between data and Monte Carlo (MC) simulation.
Any significant mis-modeling of the data threatens to affect the main measurement one wants to perform, if the simulation is relied upon in any way to derive it. So the physicist, upon observing such an effect, should spend time to investigate the cause of the disagreement, trying to figure out what "turns it on" and whether it is a confined effect or one which has an impact on the measurement meant to be performed.
The best way to study the data/MC disagreement is to try and "isolate" it: the experimentalist focuses on the region of phase space where the effect is the largest, trying to determine whether a further selection enhances it or kills it. The simulation is also put to the test by comparing its prediction with alternative background estimates, performed with different simulations or with data-driven methods. In most instances, one successfully traces back the observed disagreement to a shortcoming of the simulation, or to a mistake of some kind, some missed calibration procedure applied to either data or Monte Carlo, etcetera. But occasionally, the origin of the effect may remain unknown.
What happens from that point on is highly dependent on the kind of effect seen, its magnitude, and the level of scepticism of the experimentalist. If the effect can hardly be attributed to unknown new physics -such as if, for instance, one is just observing a flat discrepancy in the rate of the background, without specific kinematical features- it just causes the experimentalist to e.g. apply a scale factor to the simulation, and assess how much the main measurement he or she is extracting is affected: a systematic uncertainty.
On the other hand, if the level of scepticism is low, the distribution is an invariant mass of some objects observed in the selected events, and the effect is a bump in an otherwise smooth distribution, the physicist's discovery co-processor will start working in the back of his or her brain: am I observing a new particle ?
If interpreted as a departure from known physics, a new effect creates problems as far as a correct evaluation of the statistical significance is concerned. The reason is clear: the observation entails a large, unknown trials factor. The number of distributions that were tested by the experimentalist is relevant but not known; and further, if this becomes a signal of new physics that the experiment as a whole wants to stand behind of, then one should consider that the chance of finding a similar discrepancy was there whenever any one of the researchers studied any of the myriad of possible distributions that the large dataset collected by the experiment allows one to plot.
In other words, the trials factor is here a quite ill-determined, large number. In a large experiment like ATLAS or CMS, with about a thousand active physicists plotting graphs day and night, such a trials factor is likely of the order of tens, or even hundreds of thousand in a few years of operation. It transpires that it is quite likely that in the lifetime of one such experiment a four or five-sigma effect arises by sheer chance !
One example: the Vivianonium, CDF, circa 2009
The above discussion was rather abstract, yet I have in mind specific examples. One tale-telling such example is the one of the Vivianonium (thus jokingly named by my CDF colleagues after the name of the PhD student involved in the analysis, Viviana Cavaliere). This was the putative dijet resonance that was observed in CDF data containing a leptonic W boson decay. Oh, those "W + jets" events again !!! It is the third time I mention that physics process in this article, I reckon... Well, that must mean something, indeed.
So what was the Vivianonium ? The story goes as follows. A CDF group a few years ago was trying to measure diboson production (WW or WZ) by extracting a signal of the bosons' "single-leptonic" decay: one W is observed to decay into electron-neutrino or muon-neutrino pair, and the other W or Z boson is sought as a bump in the dijet mass distribution.
The W boson decays 67% of the time in two hadronic jets, and the Z does so 69% of the time: so indeed these single-lepton final states are quite a probable outcome of diboson production. Yet it is hard to extract them, because the W+jets background is large, and nasty. It is large because all strong interaction processes that produce two hadronic jets together with a W boson will contribute; it is nasty because so many are the processes, and so varied their dynamics, that one can never be totally sure one understands them perfectly (see in fact in a previous part of this article what I said above about Rubbia's discovery of the top quark, or my discussion with Andrea Giammanco on the single top discovery in the comments thread of part II).
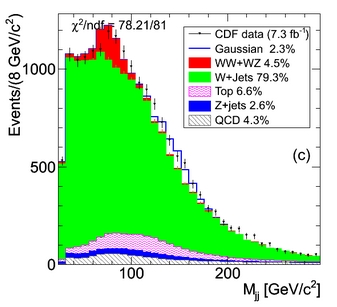The CDF experimentalists studied the dijet mass distribution of their selected data, after having applied cuts that enhanced as much as possible the diboson signal, and they did observe a nice signal of W or Z bosons there, more or less as big as they expected it. Diboson production is by now a well-measured process, so no surprise was expected there. However, while the expected bump did lay where it was due, at 80-90 GeV, the CDF colleagues observed that the data overshot the background prediction in a different mass region as well: around 150 GeV, where backgrounds were falling off, the slope of the data was different, causing a broad excess there -and a significant one. The figure on the right shows the dijet mass spectrum,with the dominant W+jets background in green and the diboson signal in red; the graph below shows instead the background-subtracted excesses due to WW/WZ (at 80-90 GeV) and to the new source at 150 GeV.
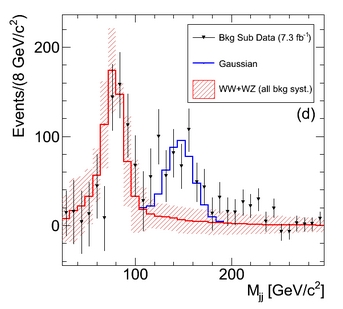I am quite sure that the authors of the search did all they could to "explain away" the discrepancy: one could play for instance with the jet energy scale or resolution, trying to change it from the nominal value by one or two standard deviations such that a deformation of data and background could bring the two back together. Or one could try and verify that the kinematics of the events in the discrepant region were not "special". Dozens of checks were conceived and performed. But the excess of data persisted. Nothing appeared to be able to wash it away.It was a very annoying thing, I imagine, to have to deal with such a large mismodeling of backgrounds in the dijet mass distribution: one which was as large in size as the diboson signal, and with a well-defined shape (i.e., not just a normalization difference of data and simulation, but a concentrated excess). The reason is easy to understand: if one wanted to extract a measurement of the diboson yield from that distribution, the presence of a unaccounted extra feature not too far away from the signal region would imply that the background was not at all well-known, so its subtraction was wrought with huge systematic uncertainties.
Maybe at that point authors started to think that they might have a discovery in their hands. A dijet resonance at 150 GeV ? That was a spectacularly seductive idea. A dijet resonance produced in association with a W boson could be a Higgs-like particle, or a Supersymmetric particle, or a technicolor object... Several exotic theories, all rather improbable, could fit such an object. To the authors of what was originally a measurement of the rate of a well-known Standard Model process it must have felt quite good to kill two birds with one stone: calling in an extra process, one could claim that systematics in the diboson yield were small!
If interpreted as a resonance, the bump had indeed some nice features: it had a roughly Gaussian shape, with a width compatible with that expected from a narrow object whose decay jets get their energy "smeared" by the detector resolution. But if interpreted as a resonance, the bump entailed a huge surprise factor...
The CDF collaboration engaged in a long investigation of the possible causes of a background mis-modeling, by using different Monte Carlo simulations, studying extreme values of jet energy scale and quark-gluon composition of jets, etcetera. In the meantime, the authors of the analysis were able to add statistics to the data: from 4.3 to 7.3 inverse femtobarns of collisions (note: the figures above are based on the full statistics of 7.3/fb). The effect of the added statistics was that the original 3.2 sigma significance of the bump raised to well above four sigma. But that was hardly a surprise: the fact that the effect was systematic in nature and not a statistical fluctuation had been evident from the start -for instance, it was present both in the electron and in the muon datasets, which both contributed to the final data sample (the leptonic W is reconstructed from electrons plus missing energy, or from muons plus missing energy).
In the end, CDF did publish the tentative resonance signal, assessing its significance at 4.1 standard deviations, but leaving open other interpretations. DZERO also searched for the signal and saw no excess in a dataset of 4 inverse femtobarns of proton-antiproton collisions. Also ATLAS and CMS looked into their first datasets of proton-proton collisions at 7 TeV energy, and observed the diboson signal but no bump at 150 GeV. Further analysis of larger dataset confirmed that observation.
Based on those additional studies, we can draw some conclusions: the Vivianonium is not a new particle but the result of some systematic mis-modeling of the W+jets background, convoluted with the details of the jet measurement procedure in CDF (I believe my CDF colleagues have drawn more definite conclusions on the matter by now, but I cannot find the relevant documentation at the moment - if possible, I will integrate it here later; but it is not highly relevant to this post anyway).
Here you can see that it is not the failure to reach a five-sigma threshold of the CDF signal what eventually writes it off: there is no doubt, in fact, that if CDF collected twice as much more data, the effect would grow to five, six, or whatever sigma significance. The effect is in fact systematic, and not statistical. What writes it off is the fact that it does not receive a confirmation from independent experiments, which are subject at least in part to different systematic uncertainties.
Fishing Expeditions and A Posterioriness
With the term "a posteriori" physicists refer to an observation which comes after having collected the data; more precisely, it is something which was not specifically intended as an object of scrutiny. The way this arises is similar to what I described above when I discussed the comparisons of data with simulated backgrounds: one finds an effect while not looking for it specifically.
A clear example of what I mean is provided by the superjet events - alas, another weird effect found in CDF data, this time in Run I. I have written maybe a hundred pages on this issue in the course of the last eight years of blogging, and I am even reluctant to link here the original posts. Rather, let me provide a short summary of the matter again here. But first let me also note that surprisingly the W+jets process is again one of the main players of this comedy ! I swear I did not plan to make such a coherent display of instances where large experiments went wrong because of ill-understood kinematics of W plus jets... It came together by chance.
Anyway, in 1997 CDF was trying to finalize the top pair production cross section measurements, based on data collected until the previous year. This was an important measurement back then, only a few years after the top discovery. To perform a cross section measurement of course CDF studied "lepton plus jets" events - ones containing a lepton, missing energy, and three or four jets, which were enriched with top pairs. To enrich that sample further in top decays one then needed to do "B tagging": identifying jets as due to the hadronization of a bottom quark was a way to enrich the sample of top decays, since the top quark always yields a bottom-quark jet. Requiring the presence of a b-tagged jet would discard the large W + jets background quite effectively.
There are two main methods to identify a jet as one originated by a bottom quark. One is called "secondary vertex tagging", and the other is called "soft lepton tagging". A secondary vertex is a feature caused by the decay of a B hadron, which travels a few millimeters before disintegrating into a few charged tracks: consequently, those tracks do not point back to the primary interaction vertex but rather to the decay point of the B hadron. A soft lepton is instead often produced by the decay of the B hadron: if inside the jet one finds an electron or a muon, the jet is likely to have been originated by a bottom quark.
It was puzzling to observe that jets containing a secondary vertex also contained a soft lepton tag much more frequently than one would expect from known branching fractions of the B hadrons; these decay to electrons or muons about a fourth of the time in total, but the rate appeared much larger. If examined carefully, the disagreement could be traced to thirteen events with this kind of "double b-tag" on the same jet.
Monte Carlo simulations predicted that one should observe only 4 such events - a roughly even mix of top pair production and W + jets, with jets originating from heavy flavour quarks (charm or bottom). A careful examination of these events then proved that they were "special": the jets had much larger energy than expected from the W+jets background and top quark decay, and the kinematical characteristics appeared quite weird.
So here we had an a-posteriori observation (I see some numerical discrepancy where I did not expect one, I check it, and find that it amounts to a three-sigmaish effect) which is the basis of observing further anomalies. The authors of the analysis of those events were deeply convinced that they constituted a first signal of some fancy new physics - possibly a scalar quark which got produced in association with a W - and wanted very badly to produce an article which described those events; yet the management of the collaboration appeared sceptical and unwilling to commit to such a publication.
The authors of the analysis studied the 13 events in a systematic way, and proved that their kinematics were by themselves weird enough that the sample constituted the discovery of some new effect. The discrepancy in the kinematical distributions of the data with background simulations could be estimated with Kolmogorov-Smirnov tests and bootstrap methods as a 6-sigma effect; however the small statistics of the sample made it hard to assess whether that was a unbiased estimate. A big controversy within the experiment arose on the details of the assessment of the significance, which was never completely resolved. You can see why: the a-posterioriness of the original observation prevented authors from coming up with a believable estimate of the overall probability to obtain data as discrepant to the background model.
Eventually, the internal conflict petered out as some publication was produced. DZERO never confirmed the effect, and no counterpart of the 13 superjet events of CDF in Run I was observed in the much larger Run II dataset. Hence those 13 events remain a sort of mystery; but it is clear that what brought them to the attention of the particle physics community was an a-posteriori observation: we see some numerical excess of very special events, and proceed to study their features, getting more excited by those features showing some discrepancy than by those that appear to agree with the background model.
Note that such approach is not bad per se, if one is looking for new physics ! The problem is that it causes one to be prevented from correctly assessing the true significance of the effect one is observing; also, maybe the bigger underlying problem is that new physics is so hard to find (if any exists at all) that such an approach is much more likely to generate false finds than anything else.
Data Manipulation ?!
The other day I quoted a passage of Rosenfeld's 1968 article where he denounced the practice of experimentalists of enhancing a tentative signal of a new particle or effect by applying unnecessary additional selection criteria. This is in fact one of the main sources of high-significance fake signals in particle physics, and it deserves to be treated separately from the others.
Let me first of all say that I have a strong belief in the honesty and ethics of particle physicists in general. We want to understand the laws of Nature more than we want a raise of salary; but even if physicists were after a raise of salary or a better position, they would never voluntarily produce a false discovery of a new particle, because they know that pretty soon their find would be disproven, ruining their reputation. What makes the game a virtuous one in particle physics as opposed to, say, medical research, is that physics is an exact science: effects are repeatable.
That said, there are of course exceptions; but much more frequent is the case of enthusiasm for the possibility of a discovery lowering the level of scepticism, and even causing one to take shortcuts to convince colleagues. In other words, if you get deeply convinced that what you have found is a real effect, you are quite likely to perform "illegal" operations to make your find more convincing.
One common operation I have already mentioned is the application of selection cuts that enhance the signal, when those cuts are not justified. The experimentalist may look at the distribution of the data on some selection variable, choosing the value of the cut such that the effect is maximized. He or she will later find reasons for choosing that particular value. Similar to the above is the selection of "good" data which Andrea Giammanco mentioned in a comment to the previous part of this article (see here). By discarding chunks of data where the effect is weaker, one enhances its significance.
Let us make a simple example: I have observed in some dataset where I expect
to see 2500 events an excess of 100: I have in fact 2600 events in total. This is a 2-sigma effect. Let's imagine I have reasons to believe that those 100 events come from a new process, and let's also admit that the data come from five different run periods, which were slightly different - some parts of the detector were in stand-by during some of the run periods, calibrations were different, etcetera.
I may decide to check how the excess divides in the five periods (each of which we assume yielded the same amount of data: we expect 500 events in each part), finding the following breakdown: 540, 520, 530, 480, 530. I may then examine more carefully the data from the fourth run period, being puzzled that it did not yield an excess. I will be likely to find that that data subset has some problem -they all do, but I have checked that one in particular! When I remove that chunk of data I get 2120 events with an expectation of 2000: this has now become an almost three-sigma effect. It is then easy for me to explain to my colleagues that my choice of removing the fourth chunk of data was based on reasonable a priori criteria.
Another common behaviour is the application of ad-hoc reconstruction methods. Imagine you find a bump in a two-jet distribution, and later discover that if you modify the algorithm that measures the jet energy you obtain a sharper peak (one such modification usually exists, given a dataset and a peak). From that point on, you will argue that your ad-hoc procedure is justified by the kind of signal you are finding, and that it works better than the standard one; it will be hard for your colleagues to convince you to prove that the method has some objective merit.
Finally, there are cases when one is observing a true phenomenon, and one wants to publish it quickly; however, there are some features in the data which are hard to explain and / or are unsupportive of that interpretation. The physicist may be tempted to hide those features, to obtain a quicker recognition of his or her find. This may lead to the extreme behaviour of "erasing" some events from a dataset ! I remember that in the era when plots were produced by hand it was not uncommon to hear stories of dots in a scatterplot (a two-dimensional graph where an event is represented by a black point) being covered by white correction ink... This is close to scientific fraud, of course; but some colleagues argue that it is a reasonable thing to do, when one is confronted with the alternative of spending months to understand an erratic behaviour of one's detector, leaving the scientific community oblivious of the new find for a long time.
---
Jump to part IV (and Summary)
Comments