Note that of the six mentioned "good quantum numbers" above only a subset are typically used. One would never go about counting the number of up and anti-up quarks in the initial and final state of a reaction, because this is not easy to do: up quarks do not have distinguishing features we can use for that purpose. The same goes for the down quarks.
S, instead, has been studied thoroughly in particle reactions since the fifties of the last century: indeed, by observing some selection rules that appeared to prevent certain reactions and allow others, physicists first invented the "strangeness quantum number", S indeed.
Strangeness was invented to explain how it was possible that certain particles would be produced with very high interaction rates in low-energy fixed-target experiments, while these particles then took a long time to decay. The high production rate implied a large value of the "coupling constant" that was involved in the production diagrams, while the slow decay implied a small value of the same. Therefore, these particles were indeed strange. Of course, the production was mediated by strong interactions (which conserved strangeness, and produced pairs of opposite strangeness), while the decay was mediated by weak interactions, which do not conserve strangeness, nor any other flavor quantum number.
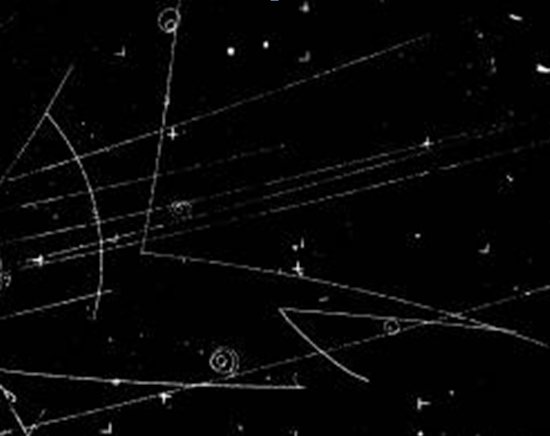The figure on the right shows a typical pair production of two "V particles": neutral ones which decayed into two charged hadrons only after traveling some sizable distance (centimeters, or even meters) in the detector. The detector is a bubble chamber, where only electrically charged particles leave visible tracks as they "condense" tiny bubbles of gas along their track. The reaction which takes place in this figure is a pion-proton collision (pions enter from the lower left) whereby two strange particles are produced in pair: a neutral kaon and a Λ baryon. Neither of these is visible in the image, since they are both electrically neutral; however their presence is inferred from their decay into other bodies. The kaon decays into two charged pions (K->ππ), while the Lambda decays into a proton-pion pair (Λ->pπ). Note that the Lambda contains a strange quark, while the k-zero contains an anti-strange one: +1 -1 = 0, and the strangeness of the final state is indeed equal to the strangeness of the initial state (0, since neither pions nor protons contain strange quarks).The use of these flavor quantum numbers is not so widespread nowadays: we just describe the processes by the exchange of mediators of the strong or weak or electromagnetic force, and we know the properties of these interactions. So top quarks are produced in particle-antiparticle pairs by the strong interaction (they might be produced in pairs by the flavor-conserving electromagnetic interaction just as well, but the electromagnetic interaction is way less intense than the strong one, so we neglect that).
However, a single top quark may also be produced in hadron collisions, if the mediator is a weak W boson. The fact was well known before the top was discovered, but at the Tevatron in Run I (1992-1996) nobody cared to look for single top quark production: it was too hard to detect it.
Note that despite the weak interaction of single top production is weaker than the strong interaction producing top pairs, the fact that only one top needs to pop into existence plays in favor of the weak interaction rate: at the Tevatron it is much more likely to get a collision with an energy release of 180 GeV (the minimum necessary to produce one top quark) than one with an energy release of 350 GeV (the minimum needed to create a top quark pair). And at the LHC, which has 4 times more total collision energy, this is still a factor. The non-linear behavior of the probability distribution to find quarks of suitable energy in the proton makes the comparison a difficult one, though.
Handwaving arguments are short-lived in the field of exact sciences such as particle physics, so in order to get a precise picture one needs to compute the real production cross sections with the tools of quantum field theory. We then learn that both at the Tevatron and at the LHC single top quarks are produced roughly twice less frequently than top pairs.
Now, since the top quark was studied at the Tevatron in run I with some detail (measuring the production rate with a 20% uncertainty, the mass with a 3% uncertanty, and other properties), one might well ask why single top was not seen back then, and its discovery had to wait until well into run II.
The problem is that when a single top quark decays, it produces a much less striking signature than when a pair of them does. The top may decay into a W boson and a b-quark jet, so the final state includes these bodies as well as another b-quark and maybe a third jet. This "W+2/3 jets" signature is mimicked by the simple production of a W boson in association with heavy flavoured jets, which has a much larger rate. The signal to background ratio is then very small, and this, combined with the small absolute production rate, made single top invisible at the Tevatron in Run I.
At the LHC things are of course easier, because the larger collision energy grants a much larger production rate of single top quarks. Take the latest result by the ATLAS collaboration as an example: by applying rather straightforward selection cuts on discriminating kinematic variables describing the observed properties of the events they are capable of isolating a striking signal in their 5 inverse-femtobarn dataset of 2011 collisions.
The figures below show in blue the single top contribution (mainly contributed by the so-called "t-channel" production diagram, but that is a detail I will leave out of this post) towering over all backgrounds (in other colours). Note in particular how the top quark mass can be well reconstructed from the three objects that the top quarks decayed into: a charged lepton (electron or muon), a neutrino, and a b-quark jet.
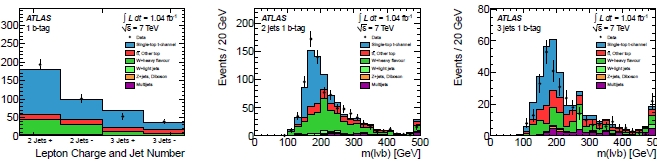
Some details on these plots: the histogram on the left shows the data (tiny black points) divided into four categories, depending on the charge of the charged lepton and the number of jets of the event. From the figure it is evident that top quarks of positive charge are produced more readily in proton-proton collisions: no surprise -the initial state has two units of positive charge, and this reflects in the higher probability that positive top quarks are produced. The histograms in the center and right panels show the reconstructed mass distribution for subcategories of the data on the left, but they include data not yet selected by the invariant mass cut which one would obviously want to apply to increase the signal purity: this allows to see how the single top signal is well separated and reconstructed.
In the end, the most performant selection is never a cut-based one, but a multivariable approach of some kind. Indeed, ATLAS uses a neural network to select single top candidates in an effective way, and it is that sample which is used for the cross section determination.
They thus produce a cross section measurement (83+-20 picobarns) in good agreement with theoretical calculations. The document describing the details of the search is available online here.
Comments