The simplest collision is that between two objects that possess a spherical symmetry. This can be a helium atom or a billiard ball. The machinery for dealing with collisions of macroscopic objects is relatively well developed. Smaller objects, like hydrogen atom, for example, exhibit rather different behavior. The key to understanding the differences between billiard ball and atomic collisions is the idea of an interaction potential of the system. Stated otherwise, ‘Do (and how) the two billiard balls/atoms know about each other?’. This turns out to be a very important question to ask. Billiard balls are certainly easier to understand. From our everyday experience we know that as the Q-ball approaches the 8-ball neither of the two exhibit any deviations from their trajectory. As far as we can tell the collision itself is ‘instantaneous’ after which the balls bounce off each other. Interestingly enough, such a naïve picture, called a ‘hard-sphere potential’, proves to be quite insightful and is used for simple molecular collision analysis. In reality atomic/molecular collisions are much more complex. As the two atoms approach one another they ‘feel’ each other’s presence before the distance between them gets to an order of a few Angstroms – the typical length of a chemical bond. This naturally leads us to now classic E. Rutherford’s experiments that employed He2+ (α particles) as projectiles and gold atoms as targets. After careful analysis of how many He2+ particles were scattered into a solid angle (dΩ = sinθdθdφ expressed in spherical coordinate system), Rutherford was able to determine the interaction potential between an α particle and Au atom. This so-called inversion procedure partly earned him the 1908 Chemistry Nobel Prize and wrote that first chapter of a modern introductory chemistry book about the existence of a nucleus and all that other ‘obvious’ stuff.
Study of collisions culminated in yet more Nobel Prizes. Particle physics was practically born out of high-energy atomic collisions that produced otherwise hard-to-generate subatomic particles. M. L. Perl from Stanford and F. Reines from UC Irvine, for example, shared a 1995 Nobel Physics Prize for ‘…experimental contributions to lepton physics…’. Furthermore, perhaps one of the most exciting experiments of the past decade will focus on a very-high-energy collisions between protons in the hope of finding the elusive Higgs boson – the last missing piece of the Standard Model. Actually, even such fundamental and well-known concepts as Maxwell – Boltzmann speed distribution are rooted deeply in molecular collisions. Successive atomic/molecular collisions bring a system into equilibrium that can then be characterized by surprisingly few parameters – as few as three, i.e. temperature, pressure and volume, in the case of an ideal gas – an incredible simplification from ~1023 parameters implied by the integration of classical equations of motion! Such an advantage of statistical mechanics, however, can turn into its biggest drawback, namely averaging. A lot of information can be gained by being able to peer at individual molecular collisions. Experimental difficulties associated with obtaining single collision conditions were not overcome until 1950s though. The results of these studies were of such a fundamental importance that a 1986 Chemistry Nobel Prize went to D. R. Herschbach, Y. T. Lee and J. C. Polanyi for ‘…their contributions concerning the dynamics of chemical elementary processes...’.
Field of molecular reaction dynamics, i.e. a study of molecular collisions, has experienced an extremely exciting development since 1986. Of particular interest are the so-called stereodynamic studies – studies that try to understand the geometric aspect of a collision. A schematic drawing in Figure 1 illustrates this idea rather well.
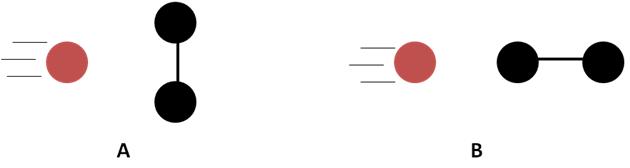
Figure 1. Two possible collision geometries: A) side-on and B) head-on approach.
Simple inspection of the two configurations suggests that the outcome (reactivity) in each case should be different. One can easily see that if the spheres in Figure 1 are, for example, billiard balls then side-on collision should make the two black billiards fly off to the sides after the collision, while the head-on geometry should lead to the rightmost ball rolling off in a roughly the same direction as that of the incoming projectile. More importantly, this is trivial to demonstrate, i.e. setting up the two different configurations shown in Figure 1 allows for a facile ‘experiment’. If, however, the spheres are a hydrogen atom colliding with a hydrogen molecule the experiment becomes far from trivial! It has been predicted theoretically[1] that for a side-on collision of H + D2 reaction the HD product is more sideways scattered than in the case of a head-on geometry[2] – something we were able to see easily with classical billiard balls! So what are the main difficulties of such an experiment?
First of all, unlike billiard balls majority of the molecules are rotating. Any field-free region of space contains randomly rotating molecules. In other words, their angular momentum vector has an isotropic spatial distribution. It has been shown, however, that the presence of a (polarized) electric field can help ‘order’ the molecules. To understand this, consider a diatomic molecule like H2 in a j = 2 rotational quantum state.[3] As any introductory quantum mechanics book teaches us, every j level is (2j + 1) degenerate. For j = 2 case this corresponds to five degenerate sublevels, namely mj = ±2, mj = ±1 and mj = 0. A pictorial representation for j = 2 case is shown in Figure 2.
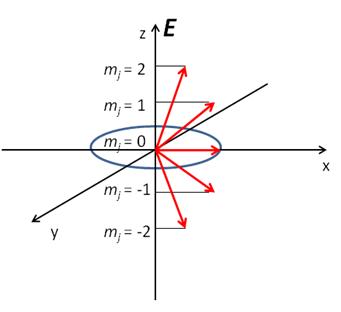
Figure 2. Quantization of the projection of vector j along E, electric field vector. All vectors precess around z axis, but only one such precession (for mj = 0 state) is shown for clarity.
This is yet another typical quantum mechanical picture: the projection of j is quantized along a particular axis. (In this case it is the electric field vector E which is chosen to coincide with z axis.) Since all the mj levels are degenerate they are equally populated. Recall also that for a diatomic like H2 the rotational angular momentum j is perpendicular to the bond axis. Hence, if the H atom projectile approached D2 molecule along, say, z axis it would ‘see’, on average, a whole range of various collision geometries. The first step in implementing the ‘gedanke’ experiment illustrated in Figure 1 would thus be a population of one particular mj level, instead of having an equal distribution over all of them. One such experiment was done on a nitrogen molecule, N2, that was excited from its j' = 0, mj' = 0 level into j = 2, mj = 0, ± 2 states.[4] More recently this laboratory has pumped H2 and its isotopes to j = 2, mj = 0, ± 2 rotational levels.[5] Both of these experiments employed a technique called Stimulated Raman Pumping (SRP) that uses two photons to drive a molecule in j', mj' state into j = j' ± 2 and mj = mj', mj' ± 2 levels where the latter selection rule, namely mj = mj' is valid for linearly polarized light while mj = mj' ± 2 holds true for circularly polarized light. The use of SRP (or any other two-photon process) is necessary since molecules like N2 and H2 that do not possess a permanent dipole moment cannot absorb one infrared photon – yet another selection rule dictated by quantum mechanics. In short, population of one exclusive j, mj state serves to align (to use a technical language) a molecule as can be seen from Figure 2: for any j, mj = 0 state the angular momentum vector j will only precess in the xy plane. Thus, if D2 molecule is in a j = 2, mj = 0 state then the angular distribution of the resulting HD product from a H + D2 reaction is certainly not going to be the same for two different H atom attack directions, e.g. z axis versus x axis approach. Fifteen years after SRP technique has been used to align N2 molecule we are finally in a position to carry out the actual H + D2 à HD + D reaction where D2 molecule is aligned! We are currently working in this direction and hopefully such a clear idea illustrated in Figure 1 will soon be performed experimentally for the simplest bimolecular reaction!
Collisions can tell us a lot about the world around us. Part of the reason for doing such complicated experiments is the joy of pushing the frontiers of chemistry. Most of all, however, one does experiments because this is what science is. One should never take anything seriously until one does an experiment. If it does not disprove the proposed idea, a new way of thinking about a certain phenomenon can be adopted. On the other hand, one should be also prepared to abandon the idea as soon as an experiment is carried out that disproves it! For now we must wait for the results of the above described experiment, because until then, albeit predicted theoretically, we cannot know the effect of reagent alignment on the outcome of a H + D2 reaction; according to Max Planck, ‘Experiments are the only means of knowledge at our disposal. The rest is poetry, imagination’.
[1] - J. Aldegunde, M. P. de Miranda, J. M. Haigh, B. K. Kendrick, V. Saez-Rabanos and F. J. Aoiz J. Phys. Chem. A 109, 6200, 2005
[2] - the use of D2 instead of H2 makes the identification of the reaction product, HD, easier. Otherwise H2 and D2 are chemically equivalent.
[3] - for the main purpose of this essay it is not necessary to specify the vibrational and/or electronic quantum numbers.
[4] - G. O. Sotz and R. L. Farrow J. Chem. Phys. 101, 4682, 1994
[5] - N. C.-M. Bartlett, D. J. Miller, R. N. Zare, D. Sofikitis, T. P. Rakitzis and A. J. Alexander J. Chem. Phys. 129, 084312, 2008; N. C.-M. Bartlett, D. J. Miller, R. N. Zare, A. J. Alexander, D. Sofikitis and T. P. Rakitzis Phys. Chem. Chem. Phys. 11, 142, 2009




