Snarky Puzzle Action Jackson 5 Answers

Asking a specific question which has a specific answer is the sign of fertile soil instead of another shovel full of fertilizer. One question leads to variations on that query. Even dull looking questions can be informative. Snarky puzzle answers usually has four problems, but the fifth installment has a bonus fifth problem.

Aug. 1,2011: Shot in the Head

Snarky Puzzle

Develop a small, experimental film of all this spin stuff. The current is scurrying along the z axis, so let it run from (-1, 0, 0, -0.1) to (1, 0, 0, 0.1) [at 1/10 the speed of light]. Pick an arbitrary point out in the xy desert, say .2, .4. Use equations 7 and 9 to drive the animation.

The Background

This problem emerges from a discussion of current-current coupling by Feynman. For static, stay-at-home charges, the situation is simple: multiply current densities together and be done with it. If the currents move at low speeds, the current density is nearly the entire story. "The interaction between two currents always involves virtual photons," according to Feynman's "Lectures on Gravitation", p. 33.

There is a high cost for an odd label such as a virtual photon. Other examples include imaginary numbers which never sound real ever. Complex numbers will always be difficult. This question tries to illuminate the physics fairy dust known as virtual particles.

The Answer
Spin 1 virtual interaction current:
$(-J_x^2 - J_y^2, 0, 0, \pm J_x ~J_y)$
Total spin 1 current:
$(\rho^2 -J_x^2 - J_y^2 - J_z^2, 0, 0, \rho J_z \pm J_x ~J_y)$

Spin 2 phase:
$(-J_x^2 - J_y^2, 0, 0, \pm 2 J_x J_y)$
Total spin 2 current:
$(\rho^2-J_x^2 - J_y^2- J_z^2, 0, 0, \rho J_z \pm 2 J_x J_y)$

Animation of currents for rho -1 to 1, Jz: -0.1 to 0.1, Jx=0.2, Jy=0.4:
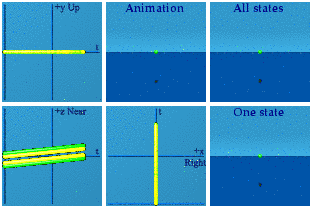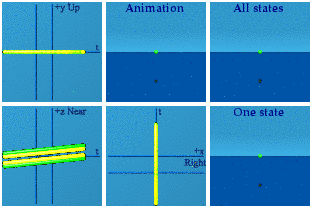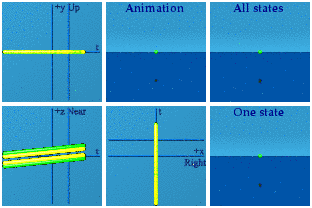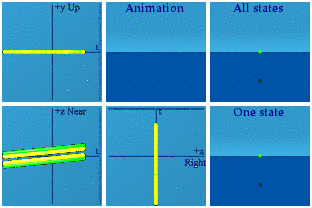
$\\(0.99 \rho -0.20, 0, 0, .1 \rho - 0.08) \\(0.99 \rho -0.20, 0, 0, .1 \rho + 0.08) \\(0.99 \rho -0.20, 0, 0, .1 \rho - 0.16) \\(0.99 \rho -0.20, 0, 0, .1 \rho + 0.16)$

[point of clarification: this is not a current, but a current-current interaction, the product of two currents. The Lorentz invariant scalar shows up in Lagrange densities. When one then applies the Euler-Lagrange equation to the Lagrangian, one takes the derivatives with respect to a current density, leaving one current density standing in the subsequent field equations.]

The Discussion

The scalar interaction term is the same, even if they are about different types of spin. The contribution from the virtual current to the scalar is negative definite - it must be less than zero for non-zero Jx and Jy. The virtual current shifts the total current.

Both sides of the z mirror are employed. There is nothing in the Jx or Jy columns, no current spontaneous generation, the mice out of straw magic trick. Everything maps back to the current along the z axis.

Animation hides data before our eyes. The events plotted in complex planes are distinct. The symmetries over the z axis can be pointed out.

In the animation, one point dominates them all. We take pride in our ability to see in 3D, but we will miss much of what happens along that axis. One must be cautious in what we claim to see at one time. Such is the plight of analytical animations: information can be hidden right in front of our eyes.
Aug. 9, 2011: Justifying The Love For The Strong Equivalence Principle

Snarky Puzzle

Work with a pathological potential:
$A = (t^2, -2x, -.4 y^3, -.2 z^2)$
Calculate:
$\\ \nabla \times A \\\nabla \times A - (\nabla \times A)^* \\A \times \nabla \\A \times \nabla - (A \times \nabla)^* \\\nabla^* \boxtimes A \\\nabla^* \boxtimes A - (\nabla^* \boxtimes A)^* \\A^* \boxtimes \nabla \\A^* \boxtimes \nabla - (A^* \boxtimes \nabla)^*$
This is not as bad as it appears: do it one time, the rest are variations in the signs of different terms. Take the group U(1) pointed in the direction of (1, 2, 3, 4) and feed that group into these eight quaternion polynomials. There should be one obvious property of the ones where the gauge happens to be equal to zero.

The Background

Massless means what? Easy, the opposite of things with mass. OK, then mass means what? Use the opposite of the first question. Run this cycle until exhausted.

The Answer

The potential is not at all pathological. Notice:
$\frac{\partial \vec{A}}{\partial t} = \vec{\nabla} \phi = \vec{\nabla} \times \vec{A} = 0$

Half of the equations are always zero. The other half would blink at the spatial origin in some kind of pattern. One needs to be more odd to be interesting.

The Discussion

I puzzled over an interesting variation to the dull question as asked. Any quaternion function could be viewed as the result of the derivative of some potential, if someone worked hard enough to find the potential. Let's ask a simpler question: compare the analytic animation of U(1) to U(1) where the scalar has been set to zero. Here it is:

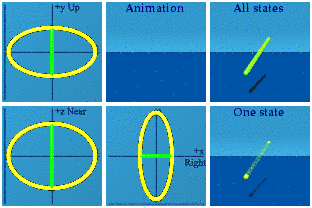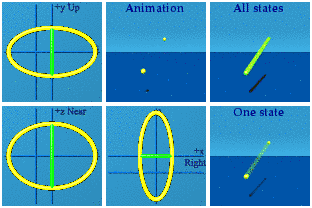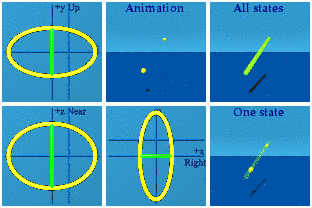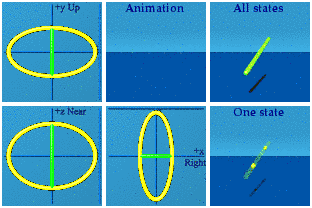
When the scalar is set to zero, its animation blinks. There is only one moment in time where there is information about the function. That one moment is now. At any other time, there is no information available. Perhaps anything that travels at the speed of light blinks in a quaternion animation. Neat if true, but the jury remains in deliberation.

Aug. 16, 2011: Visualizing Quantum Interference

Snarky Puzzle

Supersymmetry has superpartners to build super friends between particles that take different amounts of time to jog around a circle. Animate this:
$A=(cos(t), 2 sin(t/2), 3 sin(t), 4 sin(2 t))/\sqrt{30}$
Notice how the tx takes 4 $\pi$ to get back to go, ty needs 2 $\pi$ , and tz zips around in $\pi$ radians. If you like a three-way as much as I do (in theory at least), please discuss.

The Background

The supersymmetry hypothesis hopes to double the number of particles in the knowable Universe. Every boson will get a super fermion friend, while every fermion gets a super boson buddy. Those that take the normal 2 $\pi$ to get around can pair up with those needing twice as much rotation that requires this super symmetric math.

Do these super symmetry nerds ever watch diving in the Summer Olympics? There are three axes one can rotate around at different rates.

The Answer

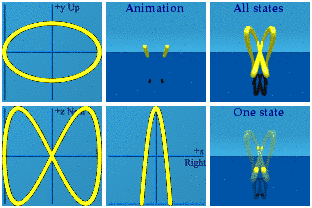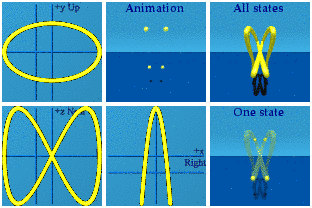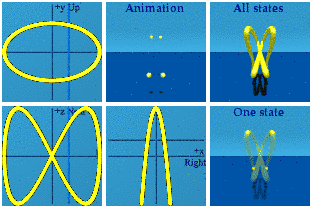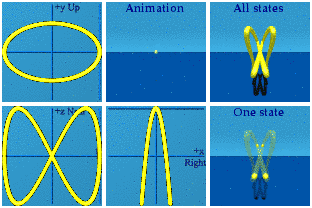
The Discussion

I can imagine the "never see nothing" defense of spin in quantum mechanics. Half integral spin is beyond the reach of human imagination, so don't try. Such an approach bores me. I would rather play, burning through a few million quaternions.

Spin 1 is like one circle, not a surprise. Spin 2 does a figure 8. Spin ½ is a windshield wiper. Spins can point in different directions.

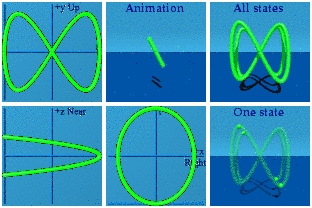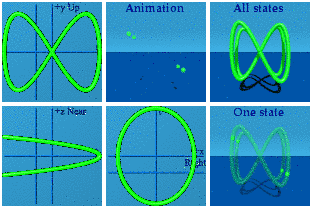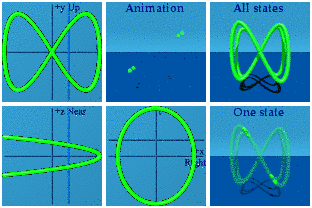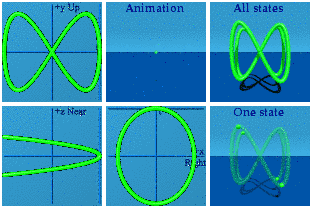
Just for fun, watch these two interact by taking the product.

These are animations of amplitudes. Those are hidden from view in the world of quantum mechanics. What we can see, on average, are the norms formed from those wacky amplitudes:

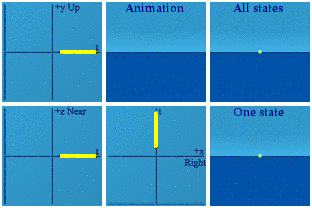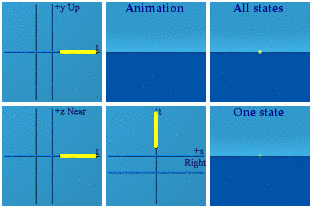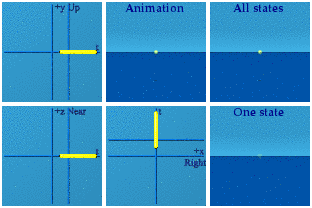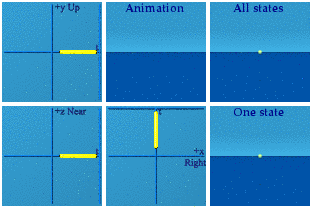
There Nature goes again, hiding her data on us.

Lab tech side bar: I am not a theory guy who can talk precisely about what is currently going on in the subject. I am a lab tech who likes to get and record large amounts of data. I wrote the software that generates these animations. It writes out to a separate file both the command run and all the quaternions generated by the process. It is a good sign that I need a few thousand data points when blogging about an issue in particle physics, a science based on more data than any other.

% cat 4.three_cycles_product.povray.100.1000.numbers | head -3
-0.4500377972303902 0.1025956024286945 0.8415039263966434 -0.0156414163467514
-0.4500377972303852 0.1025956024280495 0.8415039263981476 -0.0156414163456289
-0.4500377972303836 0.1025956024277916 0.8415039263987488 -0.0156414163451808
% cat 4.three_cycles_product.povray.100.1000.numbers | wc -l
3200

Aug. 23, 2011: Steven Weinberg and I

Snarky Puzzle

Here are the other three GEM field equations:
$\\ \frac{G \hbar}{c^5}(\frac{d A_x}{d t} - c^2 \frac{d A_x}{d y} - c^2 \frac{d A_x}{d z}) = 0 \\ \\ \frac{G \hbar}{c^5}(\frac{d A_y}{d t} - c^2 \frac{d A_y}{d x} - c^2 \frac{d A_y}{d z}) = 0 \\ \\ \frac{G \hbar}{c^5}(\frac{d A_z}{d t} - c^2 \frac{d A_z}{d y} - c^2 \frac{d A_z}{d y}) = 0 \quad eq. ~3-5$
Find the answers to these three equations. Look to 1/R for inspiration.
To my eye, the solutions are beautiful, nice variations on a 1/R potential. One up on general relativity. I don't get to say that everyday :-)

The Background

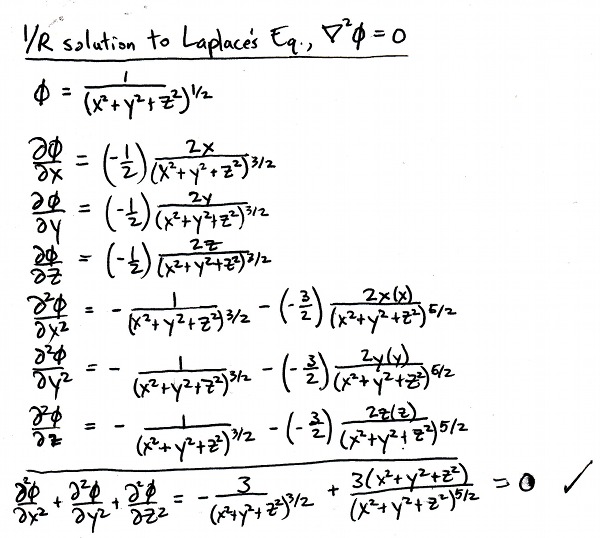
I don't recall the details of when and where I first wrote out the proof that a 1/R potential solves Laplace's equation, $\nabla^2 \phi = 0$ . It is a rite of passage into the mathematical intellectual elite. Elite does not mean better or way smarter. It means rare, something only a sliver of the population has the skills to then put the time and effort required. I will redo the calculation here by hand:

Those cancellations still feel like magic.

The Answer

The problem looks the same, with a variation of a sign flipping t, so give that a try as before.

The Discussion

If anyone has seen this differential equation or its solution put to use in any context, please give me a shout out. This solution is cool and compact, a relativistic variation on the garden variety 1/R potential.

Aug. 30, 2011: Blog on Weekly Blogging

Snarky Puzzle

Go to a reference library. No wait, don't bother. Sit down in front of a computer like you are right now. Open up another tab in your browser. Go to WolframAlpha.com. Type in: (Age of the Universe)/(Planck time). Save a tree and commit the number to memory. Now type in: (radius of the observable universe)/(Planck length). Notice the ratio between the two numbers. Then skeptically ask: (mass of the universe)/(Planck mass). Ramble about whether you think that number should be bigger or smaller than the other ones. Welcome to the world of dimensionless Planck ratios.

The Background

In my first stumble at doing theoretical physics back in 1989, I recall babling about making every number used dimensionless. Here is that idea made real.

The Answer

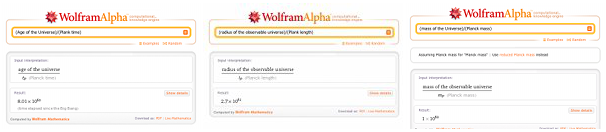Age: 8.01 x 10⁶⁰
Radius: 2.7 x 10⁶¹
Mass: 1 x 10⁶⁰

The Discussion

Everything runs away from each other at near the speed of light. Since there are three ways to run, the distance of the observable Universe is three times the age of the Universe. A simple bit of cosmology.

The mass of the Universe is the subject of ongoing studies. It shows up with one significant figure and no error bars. It looks so certain, but does not show its citations.

It was nice that the dimensionless Planck ratio mass was less than that of time, just like I had guessed.

Doug

Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser
This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.

Bet against the Higgs being found, buy the t-shirt

Next Monday/Tuesday: Deriving the Maxwell equations with Quaternions

Related articles

Comments

Know Science And Want To Write?

Donate or Buy SWAG