RETRACTION: Deriving The Unified GEM Field Equations (5/5)

RETRACTION: I have decided to retract three blogs (Deriving … 4/5, 5/5, 6/5+1). I was unable to figure out a reasonable statement concerning gauge symmetry. When the blogs were initially written, I focused on the field equations, mainly the Gauss-like law, and ignored the force equations entirely. Finding a solution that works with the the field and force equations were not looked for. A consistent proposal should do all three things (fields, forces, and solutions) with grace. I have concluded it is not possible to achieve these goals with the Lagrangian as written, hence the retraction.

The diligent reader of this mini series on fields which comes to a close today will know what is coming: a Lagrange density will be defined, the Euler-Lagrange equation will be applied to create the field equations, and something will be said about gauges. This is the simplest of those seen so far, having only twelve terms in the Lagrange density instead of eighteen or twenty two. There is nothing grand about the process. No extra dimensions peak in from peek-a-boo branes. The simple math swings out the strange, making the GEM field equations glitter.

There is one word in the title, unified, that will cause controversy. There already is an equation for gravity and EM known as the Hilbert-Maxwell Lagrange density:
$\mathcal{L}_{\rm{H-M}} = \mathcal{L}_{\rm{matter}} + R +J^{\mu} A_{\mu} + \frac{1}{4}(\nabla^{\mu} A^{\nu} - \nabla^{\nu} A^{\mu})(\nabla_{\mu} A_{\nu} - \nabla_{\nu} A_{\mu})$

This is a combo meal of our two best theories for gravity and EM. There is no give-and-take between terms. Addition is not enough to claim unification.
Click or skip this reading of the blog.
It is easy enough to follow in the footsteps of failure by adding the Lagrange densities discussed so far in this mini series [IMPORTANT CORRECTION: they hypercomplex Lagrange density current coupling term must be distinct from the EM coupling term to have a force where like charges attract]:
$\begin{align*} \mathcal{L}_{\rm{EM\;source}} &= scalar(J \times A + \frac{1}{4}(\nabla \times A - (\nabla \times A)^*) \times (A \times \nabla - (A \times \nabla)^* ) \\ \mathcal{L}_{\rm{hcG}} &= scalar(J \boxtimes A - \frac{1}{4}(\nabla^* \boxtimes A - (\nabla^* \boxtimes A)^*)^* \boxtimes (A^* \boxtimes \nabla - (A^* \boxtimes \nabla)^* ) \\ \mathcal{L}_{\rm{empty\; U}} &= \mathcal{L}_{\rm{EM\;source}} + \mathcal{L}_{\rm{hcG}} \end{align*}$

A few comments on nomenclature for anyone jumping in late. The \times symbol X is for a quaternion product. The \boxtimes is for the hypercomplex or California product defined in the forth blog. It is like a quaternion product, but no minus signs are used on the road to generating four equations for universal attraction. The three players in these field equations are a 4-current density J, the 4-potentials A, and covariant 4-derivatives (upside down triangles).

The Lagrange density

for the EM source equation can be used to derive two of the four Maxwell equations: Gauss's and Ampere's laws, as done in the second post. The hypercomplex gravity Lagrange density was used to derive an updated form of Newton's field theory for gravity. Controversy in the comments section remains over whether there is enough there there to provide a differential equation for the metric. For the Maxwell equations, a metric must be supplied as part of the background mathematical structure. I have claimed there is a potential/metric theory duality for the hypercomplex field equations. Work in a flat spacetime should you choose with the static equation:
$\rho = \partial_{\mu} \partial^{\mu} \phi$

Can this equation be solved if the potential is a constant? No, those are the differentials one learned in high school.
For a spacetime that is ever so slightly curved, which is the state of nearly all of spacetime in the Universe, treat one of the derivatives as a covariant derivative:
$\rho = \partial_{\mu} \nabla^{\mu} \phi$

The upside down triangle has a connection, which if metric compatible and torsion free is called the Christoffel symbol of the second kind. Those are technical conditions used in GR. The Christoffel symbol has first order derivatives of the metric, so this equation has second order derivatives of the metric. It is this equation along with a similar hypercomplex Ampere's law equation that has the exponential metric solution. I devoted a blog to this subject, and had a friend confirm the calculation independently.

Finally there is the form of the equation derived in the forth blog:
$\rho = \nabla_{\mu} \nabla^{\mu} \phi$

This form may apply to exceptionally strong, yet static fields. I have not found a metric solution to this equation.

This blog assumes the four hypercomplex gravity equations are a valid and interesting competing alternative with general relativity.

A good unification of gravity and the three other forces of Nature would be... no one knows. Gravity and EM are not enough. There must be a clear road to the weak and strong forces. There is no pattern of unification to follow. The unification of electricity and magnetism can be spotted here:
$\begin{align*} \nabla \times A - (\nabla \times A)^* &= (0, \frac{\partial \vec{A}}{\partial t} + \vec{\nabla} \phi + \vec{\nabla} \times \vec{A}) \\ &= (0, -\vec{E} + \vec{B}) \end{align*}$

Traditionally, one does not use quaternions, saying instead the two fields are part of the same second rank antisymmetric field strength tensor. Unification of EM and the weak force is done with group theory. General relativity with its lonely Lagrange density consisting of the Ricci scalar R has turned down all proposals by the brightest minds in physics for almost a hundred years. It is time to leave that beautiful bitch at the alter. Some women are not the marrying type. See Lady Gaga's nuptial bed at the end of the video for "Bad Romance".

When climbing at high altitude, it is vital to take a gentle, indirect assent. Let's ask a different question related to mass and the other forces of Nature: what does the Higgs mechanism accomplish?
Right out of the box, the standard model has particles with zero mass for all, including the bosons. That works fine for photons and gluons, but not the three bosons of the weak force. The two W's and Z's need to gain some mass in a way that does not break the symmetries found in the Lagrange density. The Higgs mechanism leaves the Lagrange density untouched. Instead, it uses the Mexican hat trick, spontaneous symmetry breaking of the vacuum by the scalar Higgs field. Just like the game "Clue", the LHC knows by now where Professor Plum must have used the candlestick to foil high energy physicists for decades on end: 119 GeV. That is the money bet. Bookies in England won't take a bet for finding no Higgs. That is the bet I want to make, no Goddamn Particle, not now, not in the near future with 5 inverse femtobarns of data from the LHC.

The basic fields have gauge fields, using either California or quaternion products:
$\begin{align*} \nabla^* \boxtimes A &= (\frac{\partial \phi}{\partial t} - \nabla \cdot A, \frac{\partial \vec{A}}{\partial t} - \vec{\nabla} \phi - \vec{\nabla} \otimes \vec{A}) = (g, \vec{e} - \vec{b}) \\ A^* \boxtimes \nabla &= (\frac{\partial \phi}{\partial t} - \nabla \cdot A, -\frac{\partial \vec{A}}{\partial t} + \vec{\nabla} \phi - \vec{\nabla} \otimes \vec{A}) = (g, -\vec{e} - \vec{b}) \\ \nabla \times A &= (\frac{\partial \phi}{\partial t} - \nabla \cdot A, \frac{\partial \vec{A}}{\partial t} + \vec{\nabla} \phi + \vec{\nabla} \times \vec{A}) = (g, -\vec{E} + \vec{B}) \\ A \times \nabla &= (\frac{\partial \phi}{\partial t} - \nabla \cdot A, \frac{\partial \vec{A}}{\partial t} + \vec{\nabla} \phi - \vec{\nabla} \times \vec{A}) = (g, -\vec{E} - \vec{B}) \end{align*}$

No matter how the 4-derivative and 4-potential are multiplied together, the first term of the product is the same (it transforms like the diagonal of $\nabla^{\mu} A^{\nu}$ for those more familiar with tensor notation, which is not a Lorentz invariant). This is a perfect setup for a perfect cancelation. In blogs 2-4, the gauge field was wiped out first thing. This time, the gauge field is a keeper. Rewrite the Lagrange densities including the gauges [IMPORTANT CORRECTION: The current coupling term is a sum of rho phi and J.A for the hypercomplex gravity proposal.]:
$\begin{align*} \mathcal{L}_{hcG\;+\;gauge}&=J \boxtimes A + \frac{1}{2}(\nabla^* \boxtimes A)^*\boxtimes (A^* \boxtimes \nabla) \\ &= J \boxtimes A + \frac{1}{2}(g, -\vec{e} - \vec{b})^* \boxtimes(g, \vec{e} - \vec{b}) \\ &=(\rho \phi + J \cdot A, \rho \vec{A} - \vec{J} \phi - \vec{J} \otimes \vec{A}) \\ &\quad+ \frac{1}{2}(g^2 + e^2 - b^2, -2 g \vec{e} + \vec{e} \otimes \vec{e} - \vec{b} \otimes \vec{b}) \end{align*}$
$\begin{align*} \mathcal{L}_{EM\;+\;gauge}&=J \times A + \frac{1}{2}(\nabla \times A)\times (A \times \nabla) \\ &= J \times A + \frac{1}{2}(g, -\vec{E} + \vec{B}) \times(g, -\vec{E} - \vec{B}) \\ &=(\rho \phi - J \cdot A, \rho \vec{A} + \vec{J} \phi + \vec{J} \times \vec{A}) \\ &\quad+ \frac{1}{2} (g^2 + B^2 - E^2, -2 g \vec{E} + 2 \vec{E} \times \vec{B}) \end{align*}$

The phases are worthy of study. When I have a small army of grad students, I promise to do so. It looks like fertile soil to work because Poynting's vector shows up by a happy accident. For now, I will follow the rules laid down by the Einstein summation convention and ignore the phase terms.

Define the GEM Lagrange density by subtracting one from the other [IMPOERTAND CORRECTION: there is a 3-vector current due to the hypercomplex gravity current coupling term change]:
$\begin{align*} \mathcal{L}_{GEM}&= scalar(J \boxtimes A - J \times A \\&\quad+ \frac{1}{4}(\nabla^* \boxtimes A)^*\boxtimes (A^* \boxtimes \nabla) \\&\quad- \frac{1}{4}(\nabla \times A)\times (A \times \nabla) )\\ &=2(Jx+Jy+Jz)+ \frac{1}{4}(e^2 - b^2 + E^2 - B^2) \end{align*}$

The gauge field is gone due to a perfect cancelation. There are 4 distinct field strengths, 4-derivatives of the 4-potential A. Each one is gauge dependent. That means they are relevant to particles that have mass and are unable to travel at the speed of light. Yet the overall Lagrange density is invariant under any gauge choice because of the cancelations. All of this happens at the level of the Lagrange density, not the solutions.

As done in previous blogs, the Lagrange density must be written out in the component parts. We have been there, done that, so copy in the results:

We need to toss in a minus sign for each of these to get to the GEM Lagrange density. Only the mixed terms have opposite signs so will cancel. We are left with only squared terms [correction: location of first '(' per comment below] [IMPORTANT CORRECTION: the GEM Lagrangian has a 3-vector current density]:

$\begin{align*} \mathcal{L}_{GEM}&=2(Jx+Jy+Jz)\\ \ &\quad\frac{1}{2}(-(\frac{\partial Az}{\partial y})^2 - (\frac{\partial Ay}{\partial z})^2 + (\frac{\partial Ax}{\partial t})^2 + (\frac{\partial \phi}{\partial x})^2 \\ &\quad \quad - (\frac{\partial Ax}{\partial z})^2 - (\frac{\partial Az}{\partial x})^2 + (\frac{\partial Ay}{\partial t})^2 + (\frac{\partial \phi}{\partial y})^2 \\ &\quad \quad -(\frac{\partial Ay}{\partial x})^2 - (\frac{\partial Ax}{\partial y})^2 + (\frac{\partial Az}{\partial t})^2 + (\frac{\partial \phi}{\partial z})^2) \end{align*}$

Focus on the terms with a phi:

Apply Euler-Lagrange:

Summarize by rewriting using fields:

Focus on the Ax terms, there are only three:

Apply Euler-Lagrange:

Summarize:

Compare the two laws:

There is a lot to talk about. Actually, the issue is that there is so little to talk about. Front row and center is the zero that is the current coupling term that is not there. Whatever this is, it cannot be about EM, there is no home for charge. Physics doesn't need Maxwell II since the Maxwell equations have stayed solid all these years. The GEM field equations don't encroach on that turf.

If there is no mass density, it cannot be about gravity. Gravity requires big honking sources. Zero is not big.

Bring together a force where like charges attract with other forces where like charges repel creates a conflict. A charge cannot do both. The zero looks good.

The GEM field equations are not grand, that was promised. They do accomplish two feats. The first is to offer an alternative to the Higgs mechanism. A gauge field is included and cancelled away in the same Lagrange density. That is what GEM does. The second bit of mathemagic is a field theory justification for the equivalence principle. The terms that use the California product house gravitational mass. The terms that use the quaternion product house inertial mass. The two always exactly cancel. Nice.

By repeating this exercise with a unit quaternion, the work will apply to a force that has SU(2) symmetry, the weak force being the obvious candidate. One could even plug in two quaternions, A* B, in the hopes of reaching out to SU(3) symmetry, but I am doubting that result since demanding the norm be one means there are not eight degrees of freedom. There is always something to struggle with.

Here is a property that surprises me to this day, and I have no idea what it means, but it sounds deep. There are technical quantum field theory books devoted to gauges. It seams like many important Lagrange densities are invariant under a gauge transformation, examples including the Hilbert and the Maxwell Lagrange densities. All the Lagrange densities that have appeared in this mini series have been invariant under a gauge transformation. The GEM field equations are also invariant under a gauge transformation, unlike the Einstein or Maxwell equations. What does it mean that the field equations are independent of a gauge choice? If being invariant under a gauge transformation is a deep idea for Lagrange densities, that might also be the case for field equations.

Doug

Snarky puzzle: I doubt it is meaningful, but do the sum of the gauge dependent Lagrange densities instead of the difference. Practice, practice, practice. Someday those equations might solve a deep mystery. Or not.

Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.
Now that you completely understand what is on these simple garments, bet against the Higgs being found and buy the t-shirt

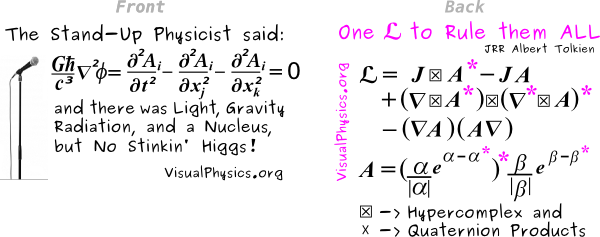
Next Monday/Tuesday: Snarky Puzzle Answers VI, including showing E² - B² is invariant under a Lorentz boost (well known), and e² - b², Doug might be wrong, will have to calculate and see.

Related articles

Comments

Know Science And Want To Write?

Donate or Buy SWAG