In truth, I was hoping I could have internet on board, which would have allowed me to track the radiation measurements on the map as the plane flew its course: this is one of the coolest features of the RadiaCode, in fact. Unfortunately, my plan went south as no internet was provided on board. Still, I could track the radiation measurement as a function of time, which roughly gives some indication of the position along the route. In fact, the radiation log shows this profile:
As you can notice, there is a first 1-hour-long spike due to the short Venice-Zurich flight; and then a longer plateau (with a few rate changes along the way) during the long-haul flight from Zurich to Tokyo.
It is interesting to note that the radiation levels are over one order of magnitude higher than those on the ground. Also, the RadiaCode is sensitive enough to report where the plane changed its altitude - you can see a few small steps in the long flight, on top of a more smooth variation that is mostly due to the night-time effect (we get slightly more radiation from one direction in the sky than from the other). Radiation is strongly dependent on altitude because of the way cosmic ray showers develop in the atmosphere.
By the way, if you look more closely in the graph above, you can see that before the VCE-ZRH bump there is a much sharper, higher spike. That is when I passed the device under the x-ray scanner at the Venice airport. Interesting to note is the fact that I found out the machines that scan luggage there leak a significant amount of x-rays in the surrounding area. No good news for the personnel operating them!
Anyway, the more interesting thing to do if you are not an airport employee is to examine the energy spectrum of the recorded radiation over the entire trip. There, you can see something like this:
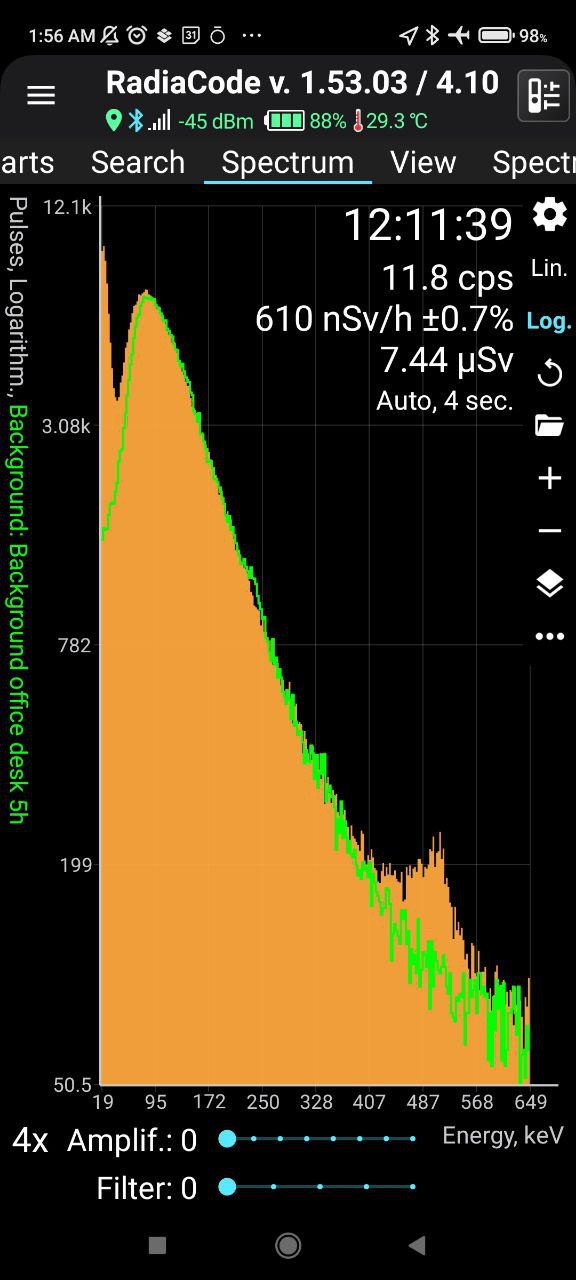
The data collected during the flight is shown by the brown histogram, while the green empty one shows a rough background estimate from data collected on the ground. The zoomed-in graph shows recorded counts of photons in the energy interval from 19 keV to a few hundred keV.
There are three features that stick out here. The most evident is a very tall peak at very low energies - a couple of tens of keV. The second is a small but very clear peak around 511 keV. What are they? I must say I am not quite sure about the origin of the first one (I need to check my hypothesis), so I will abstain from commenting on it. But I do know what the second one is: it is the product of annihilations of positrons with electrons, which produces two gamma rays of 511 keV. The RadiaCode catches some of those gamma rays and reports a bump from which you can count how many positrons did the trick. But where does this antimatter come from?
Anderson Would Have Been Proud
Positrons are the antiparticles of electrons. Discovered in 1932 in cloud chamber images by Carl Anderson, they have the same mass and share many other features with electrons, but they have opposite electric charge - a positive unit, while electrons are negatively charged. In our atmosphere, poisitrons get created together with electrons when high-energy gamma rays travel close to a nucleus of Nitrogen or Oxygen: the "pair production" process can then take place, where in a disappearing act the photon transmutes in matter and antimatter, while also giving a small kick to the nucleus. But where were these energetic gamma rays coming from in the first place?
Our Earth is constantly bombarded by cosmic radiation. This takes the form of energetic protons or light nuclei, gamma rays, and also electrons and positrons. When they reach an altitude of 100 km or so, these "primary" particles (in the sense that they are the particles hitting our atmosphere, and originating many secondaries) soon collide with the matter our atmosphere is composed of, producing a multiplication effect.
Take a very energetic proton. It may hit head-on with a nucleus of Oxygen, breaking it apart and creating a host of other hadrons in the process. About a third of the newly created particles will be neutral pions. The neutral pion is a hadron made up of a quark-antiquark pair. It is the lightest hadron, in fact, so it cannot produce any lighter hadrons in its decay. This forbids it to decay by the strong interaction; however, the quark and the antiquark inside the neutral pion can quickly annihilate (like the electron and the positron, they too are a particle-antiparticle pair, so they are allowed to do this), emitting two energetic gamma rays. The gamma rays from neutral pion decay are the most likely originators of the positrons that your plane encounters during a high-altitude flight. Another source are those produced by primary gamma rays. A third are primary positrons.
All in all, the antimatter we can record with a small radiation counter is not a lot, and it is totally harmless at this density level. But the RadiaCode can still see it, and this is really cool! When I saw the little signal I immediately looked for a smaller bump at twice the energy, as of course sometimes the annihilation of the positron with an electron will happen inside the scintillation crystal of which the instrument is endowed - in that case, the detector will record twice as much energy, as it will be able to absorb the energy of both gamma rays produced in the annihilation. But there is no peak at 1022 keV. How come?
Double-Photon Signal, Where Art Thou?
Of course, the issue is the rarity of the phenomenon. The detector has a sensitive volume of about one cubic centimeter. What is the ratio between annihilations taking place there to the number of annihilations that direct only one of the produced photons inside the cube? Answering this question is the key to understand why we cannot see a bump at 1022 keV in addition to the 511 keV one.
The calculation is practically impossible to perform exactly, as it depends on the 3D map of the material surrounding the detector: annihilation takes place where there is an electron waiting for the positron to meet it. Electrons are everywhere, but they are more numerous in heavy atoms. That is why we would need a 3D map...
We can make a step forward if we accept that most of the annihilations take place within the plane. There are two things that suggest this is a good approximation: the plane has a large mass, while the thin air surrounding it contains much less matter - so many fewer electrons per cubic centimeter. The plane also flies parallel to the ground, while positrons come in mainly vertically. So for the purpose of the fatal encounter of the pion-decay-originated-gamma-ray-originated-positron with an electron in the plane, we can jolly well consider a spherical plane, with a radius of 3 meters.
The plane is highly disuniform in matter density - much of its mass is in the external steel walls - but we won't be too much off if we assume uniform density, too. So here you have the picture: an annihilation that may direct one 511-keV photon inside our detector takes place anywhere in a radius of 3 meters (I'll pretend I was sitting exactly in the center of my spherical plane!). What is the cross-sectional area of our scintillating crystal as seen from photons traveling from a place within the sphere?
The above is a complicated question, but we do not need to answer it. Rather, we will observe that a annihilation generated inside the detector produces two photons (our target signal, whose rate we wish to estimate); and that annihilations generated outside produce only one photon in the detector at most, when the photon is directed into it or in the opposite direction (as there are two photons, and we assume they are emitted back to back in the annihilation!).
If you consider the matter from the perspective of the annihilation point things become clear: at a distance of x centimeters from the detector, the detector covers a fraction equal to 1/4*pi*x^2 of the total solid angle. That is the probability of a hit from one annihilation, but we multiply by two to account for the two photons. So 1/(2*pi*x^2), at distance x. But there are a growing number of positions sitting at a distance of x cm from the detector: indeeed, at distance x these are 4*pi*x^2! Hence we have to compute the integral of 4*pi*x^2/(2*pi*x^2) in dx from 0 to 300 cm... And this is 2x computed from 0 to 300, or 600 cm. Taking dimensions in account, we end up with the ballpark estimate that if we have one annihilation per cubic centimeter in the 300-cm-radius plane, we will record 600 single photons, and only one case of two photons.
The one-in-600 ratio we derived above glosses over a number of details that may alter the estimate by factors of two or so. E.g.: we have ignored positrons annihilating outside of the plane. Now, while the plane's external walls are thick and they present a shield from the 511 keV gamma rays we want to detect, the contribution from outside is small because of the small density of air outside. A factor of two uncertainty there is a safe one. Then we have the assumption of uniform density in the plane - certainly wrong, but accounting for the effective material distribution would not alter the calculation in a very dramatic way. The sperical assumption is probably the biggest offender here, but again, probably we are again saved by absorption effects from photons produced farther up or down the aisle.
So all in all: for every 10,000 annihilations we see at 511 keV, we might expect of the order of 20 or so at 1.022 MeV. The spectrum shows a bump that contains a signal of about 1500-2000 annihilation photons at 511 keV, which means we would expect 3 or 4 double-photon events in the data. That expectation might likely be wrong by a factor of 2, or even 4, but it is hardly off by more than a factor of 10. As the number of recorded counts from backgrounds alone in the vicinity of 1.022 MeV is in the hundreds, there is no chance to see a signal there - it is too small to make a visible difference in the background counts!
If you think the above calculation (which, by the way, was done by heart as I do not have means to write equations on a piece of paper where I am sitting at the moment - so it could well be wrong, in which case please let me know in the comments thread!) is too "handwaving" or imprecise, you probably possess the gene of the theoretical physicist. If instead you feel at ease with it, you are probably more like an experimental physicist... If you have left this post well before the end of that paragraph, you are instead not going to benefit from this classification anyway!





Comments