Note that the above does not mean that the W mass is the only reason to think that our understanding of fundamental interactions between elementary particles is incomplete. Neutrino masses and oscillations, the hierarchy problem, the question of dark matter, are all outstanding issues that at present we have no good explanation for. But when it comes to estimating quantities which are in principle calculable from other data, the discrepancy between the measured and estimated value of the W boson mass is today the single most striking example of potential imperfection of our calculations.
The situation can be pictured by the graph below,which shows relevant measurements of the W mass and the theoretical prediction. It does not take a genius to realize that the CDF result (the bottom one) and the theoretical predictions are so wide apart that one of the two (or both) must be wrong.
The same conclusion can be reached if we do not single out the latest CDF result but honestly produce a weighted average of all results; doing that is in truth tricky as some of the systematic uncertainties hidden behind those uncertainty bars are partly correlated between some of the experimental results; but we should not split hairs here when we look at the big picture.
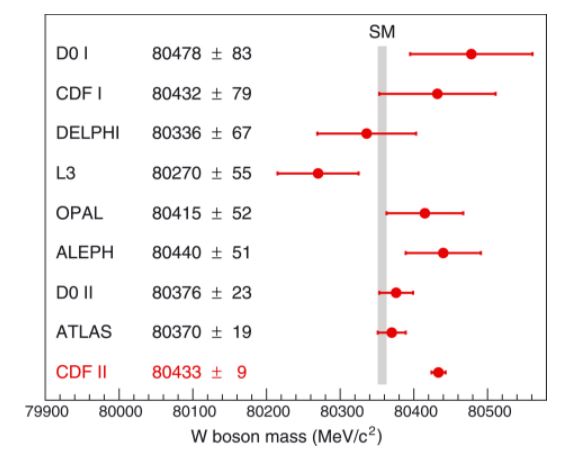
The real question, for experimentalists and theorists alike, has been a different one, and here I have been hearing statements I do not concur with, all the way to blunt assertions of disbelief, that "the CDF result is certainly wrong", etcetera. People with a Ph.D. have been producing estimates according to which the CDF result is "four sigma apart" from the others, e.g.. That is baloney, and in the rest of this post I will give a brief contribution on clarifying the matter.
When you are confronted with a set of measurements of the same physical quantity, an important issue is to understand what is their mutual compatibility. If they appear to be seriously at odds with one another, you should avoid a direct combination, pending more detailed studies of internal correlations, ill-assessed systematic uncertainties, omitted biases, or errors of the third kind. So, it does make sense to discuss the compatibility of the nine results in the graph above.
What I see many have been doing is to compute the weighted average of the eight pre-CDF measurements, and compare the result with the CDF measurement. The difference between those central values, divided by the sum in quadrature of the two uncertainties, is what we call a _pull_ - a "number of sigma", the significance of the discrepancy. This procedure is wrong by itself, and then it can be aggrievated if one mistakes the one-tailed test for a discrepancy for a two-tailed test - as if departures of the CDF measurement "toward high, more SM-discrepant values" was a sensible way to define the region of interest. But let me take one thing at a time.
When you have 9 measurements and you question one of them on the basis of their mutual compatibility, you are implicitly doing something a posteriori: you singled out the ninth measurement because it stuck out. This apparently innocuous focusing on which eight results you compare to the other one is the cause of a change of the sampling properties of the estimator of discrepancy - your pull as defined above.
What you should instead do, of course, is one of two things.
- One is to fit the nine results together, and extract the probability of the fit. This, of course, will not focus on CDF alone, and will cast the blame equally on all measurement - which is correct, of course, as we have no a priori reason to doubt on the value or uncertainty published by CDF rather than, say, by DZERO or any other of the 8 previous results. I leave this test to the reader as an exercise, as it is not the main point I want to make in this article.
- A second test you might want to do, which indeed highlights the a-posterioriness of the procedure of singling out CDF I was mentioning above, is to test with pseudoexperiments what is the distribution of pulls which you get when you take the most discrepant of the nine measurements and compare it to the rest. This will *not* be a Gaussian distribution, and your test statistic is not a proper pull - it requires calibration before you can extract a significance estimate from the observed value. Let us see how to do this.
We take the 9 experimental measurements and we assume that
1) they are all unbiased, gaussian estimates of the same physical quantities
2) their uncertainties are uncorrelated
3) their uncertainty bars as quoted are correct.
Now we sample nine numbers from the same central value - it does not matter which, so let's take 80400 MeV - with the quoted nine Gaussians G(80400,s_i), with s_i (i=1...9) the nine quoted uncertainties.
Next, we find the most discrepant of the nine random estimates, m_i*, and proceed to compute the pull as before, by first getting the weigthed average of the other eight, m_8 +- s_8, and then computing
P = |m_8 - m_i*| / sqrt( s_i*^2 + s_8^2).
As you can see we take the absolute value of the discrepancy, as we cannot in earnest decide a priori whether we will be more surprised of an upper or lower departure.
The above recipe can be repeated a hundred thousand times in the matter of a couple of seconds on my laptop. Plotting the distribution of P results in the graph below, where I have indicated with an arrow the result of doing the calculation of the pull with the actual nine measurements.
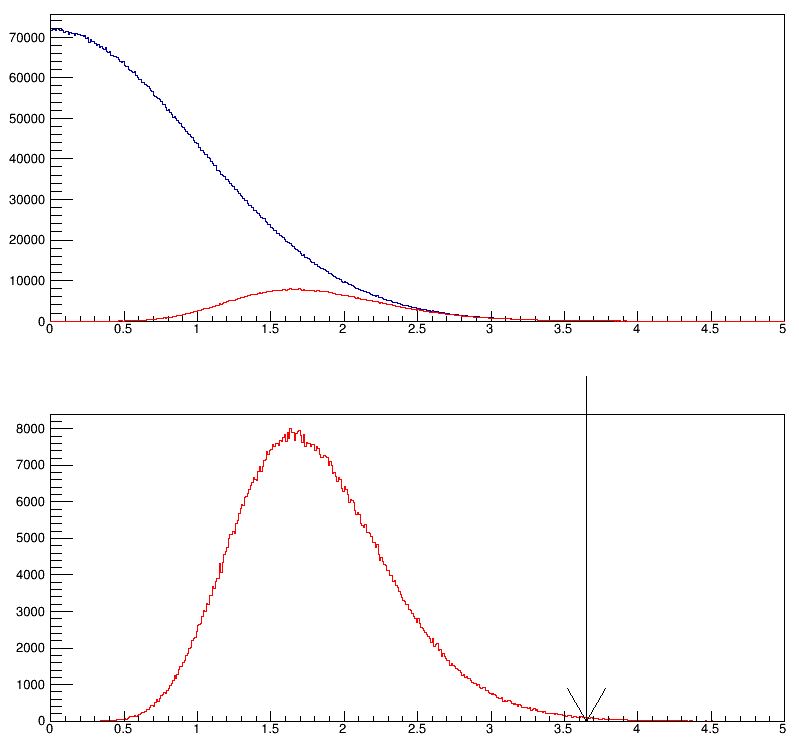
Now it is clear: the test statistic we are computing (in red) is not Gaussian like the pull computed with all possible leave-one-out combinations (in blue): it is highly skewed toward positive values, because we have been comparing to the other eight the most discrepant of the nine results in every pseudoexperiment. As a result, the pull one computes from the real data - 3.65 sigma - in fact comes from a p-value of 0.0024, which corresponds to a true significance of 2.82 standard deviations. The difference is conspicuous, as a compatibility at the level of 2.82 sigma is not enough grounds for making unsubstantiated claims of mistakes.
But there is one further detail (actually, there are others connected to correlated systematics, and they play in the same direction, but let me omit those for brevity here) which further reduces the attention level to the overall disagreement claimed of the W mass measurements. In fact, if we take the eight results that get compared with the CDF one, we see that their internal compatibility is very good, but still not perfect.
The chisquare of their combination is 8.3197, for 7 degrees of freedom. Since we are deciding to compare the previous 8 measurements to CDF and then we check the internal consistency of the two, if we start with results that are not perfectly compatible among each other (i.e., a set for which the combined chisquare is 1 per degree of freedom) we are not doing a perfectly unbiased check - we are extracting a pull by dividing by a quadrature sum of variances, and the variance of the weighted average of the 8 previous measurements is smaller than it should be, given that the combination has a chi2>1; this will produce a larger pull of which the CDF result is not guilty.
So we may take the PDG prescription of rescaling the 8 uncertainties by the square root of the reduced chisquare before we compute the pull above. The result is shown below.
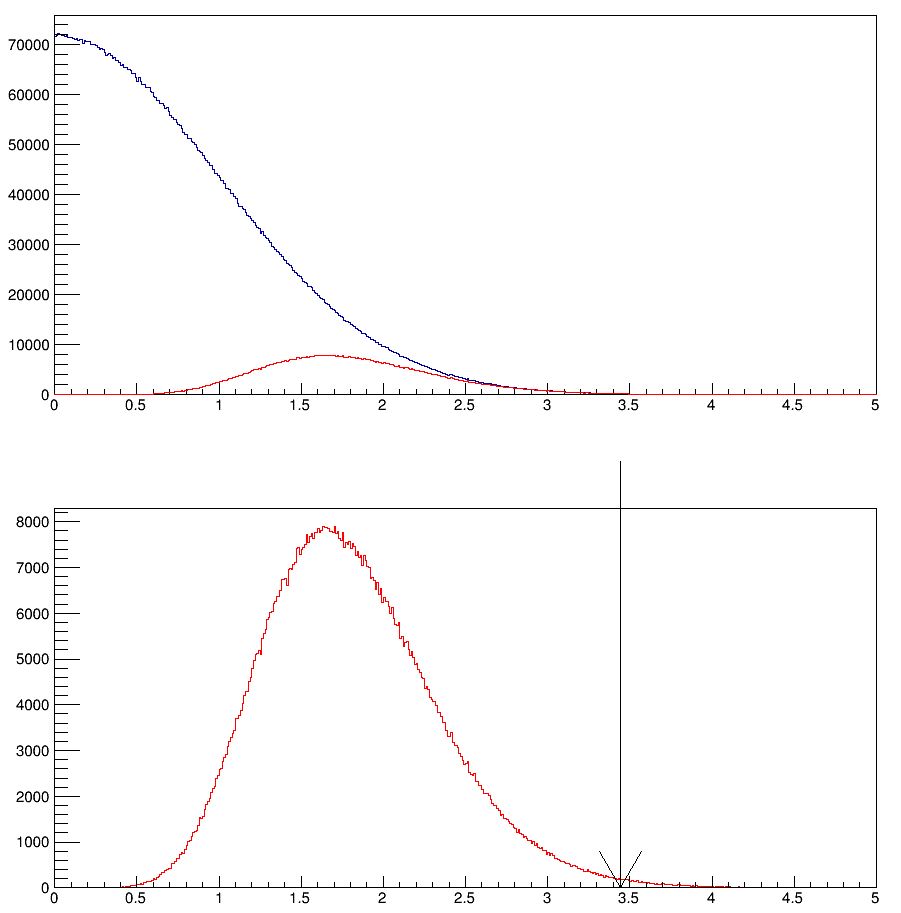
Now the CDF measurement is at a difference of 2.56 standard deviations, or a p=0.0052 effect. This is no news, people, please walk on. The real issue is thus *not* whether CDF is right or wrong, from a methodological standpoint: the issue is whether there is something wrong with the experimental measurements overall, or rather, with the Standard Model prediction.
As I wrote in a previous article here, it is perfectly acceptable to question the CDF measurement in itself, and indeed I provided there at least a couple of reasons why I believe the uncertainty quoted in that result might be underestimated. But this is a different stance from the one of using the previous eight measurements (which I am sure have their own skeletons in the cupboard) to cast doubt on the CDF measurement alone!
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from 15 institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments