Usually, before I get into the details of such studies, I make sure I provide some entry-level background for interested, but non-introduced, readers. This time allow me to point you to an introduction to weak bosons, which I wrote for another recent post. Here, instead, I will just recall a few properties of the W, the carrier of charged-current weak interactions.
Identikit of W
Name: W boson
Mass: 80.398 GeV, give or take 25 MeV
Width: 2.141 GeV, give or take 41 MeV
Typical lifetime: one trillionth of a trillionth of a second
Spin: one unit
Electric charge: one unit
Other distinctive signs: always carries aprojector
Preferred decay:(33% of the times each)
Other decays:(11% of the times, each)
Rare decays: not seen any yet.
Largest number produced: about 250 millions, Tevatron, circa 2002-2010
Responsible for: beta decay, electroweak interactions
The Radiative Decay
As detailed in the above list, the W boson has been studied in all its decay to pairs of elementary fermions (quarks and leptons, which are all particles of half-integer spin): lepton-neutrino pairs, or a quark-antiquark' pairs. Such are of course the most natural decay modes of electroweak bosons, because they do not involve any additional three-particle vertex: they can be described as the simple "splitting" of the W into the two fermions. But this is not the only thing that may happen, and in quantum mechanics everything that is not forbidden must happen!
Indeed, we may imagine all sort of Feynman diagrams which have a W boson entering from the left (if time is taken to flow from left to right, that is) and different species of particles coming out on the right. Some of these diagrams are forbidden by quantum laws, others are allowed, and they thus do occur, even if at rates which are too small to be measured.
If the above sounds abstract to you, please consider that the quantum laws are much simpler than those we humans cook up in our parliaments. Let me list a few examples:
- Energy is conserved. This prevents the W boson to decay into a top-antibottom quark pair: the W boson does not have enough energy to materialize a top quark.
- Electric charge is conserved. This explains why a neutral Z boson may decay to an electron-positron pair, while a charged W boson cannot.
- Angular momentum is conserved. This, along with other laws, prevents the W to produce an electron and two neutrinos: there is no way to make a unit of spin with three half-units.
Despite these strict laws, as I mentioned there are many possible decays which must occur, but which are suppressed by the fact that the detailed way by which the wanted final state may be produced involves additional vertices -like ones describing one particle line emitting another. So take the W decay to a charged pion plus photon final state: one boson enters from the left, two bosons exit from the right. Angular momentum is fine -one unit of spin on the left, one unit on the right (the pion has zero spin); energy is of course also okay -the final state is very light. Indeed, this decay does not violate any rule, but it does involve a more complicated kind of diagram than the simple two-fermion decay, as shown in the two panels below.
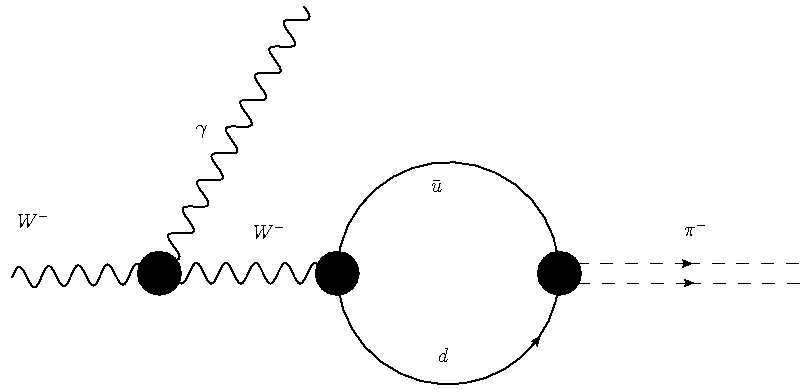
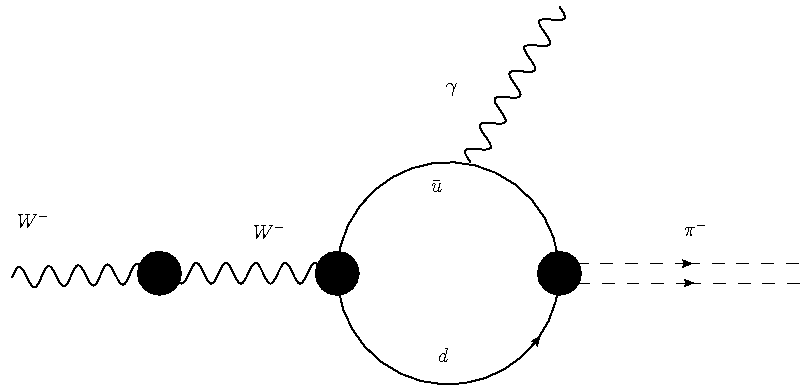
These diagrams are slightly misleading -and I apologize for that- because the black dots are not the "vertices" I have been discussing. In particular, the point where the two quarks rejoin to form the charged pion is not a vertex. All others are, however: and so, with respect to the simple
The CDF search and its results
True, one in a hundred million is rare. But the Tevatron has produced over a hundred million W bosons in the core of CDF so far! Let us compute: the W boson cross section is 20 nanobarns, and the luminosity collected by CDF since 2002 is of 6 inverse femtobarns. So if we multiply cross section by luminosity we get the number of produced W bosons: 20 nanobarns are 20,000 picobarns, or 20 million femtobarns; and 20 million femtobarns multiplied by 6 inverse femtobarns is 120 million of them W's, indeed.
The lesson we get is that if CDF were a perfect detector -hermetic, and capable to collect each and every event, and with a 100% efficiency to detect pions and photons-, we could expect to see one, or even two or three, such events in our dataset. But the above assumptions are beyond optimistic! In reality, the detector is not hermetic -how can it, since protons and antiprotons have to enter and exit on the two sides!, the collection of events withstands the hard rules of data acquisition and is subject to large inefficiencies or voluntary rejection of events with characteristics not distinctive enough, and the detection efficiency of particles is never 100%.
Furthermore, even assuming a perfect detector, we must realize that as clean and nice the W decay to a pion-photon is, it is subjected to be mimicked by backgrounds of all sorts. Photons may be faked by hadrons in the calorimeter, charged pions have no distinctive features to distinguish them from other charged tracks. Thus backgrounds will be present, and they will prevent us from being sensitive to a one-event signal! CDF, in the present search, is sensitive to a signal of 40-50 signal events, not less.
The only real smoking gun for the rare process is the invariant mass of the pair of final state objects: if the pion-photon pair comes from a W decay, the combined mass must be close to 80 GeV. This is what you can see in the figure below: the invariant mass of all selected photon-pion pairs found by CDF in a dataset corresponding to an integrated luminosity of 4.3 inverse femtobarns -most, but not quite all, the data collected so far.
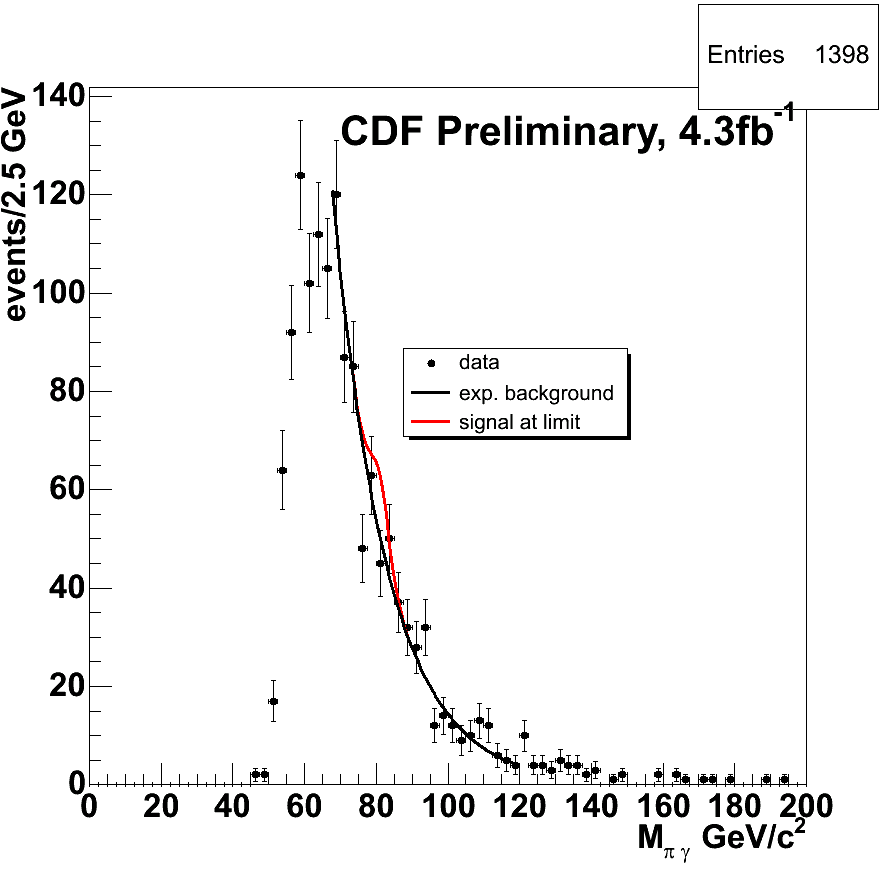
In the figure you see that there is a large number of events possessing all the required attributes of pion-photon pairs: 1400 entries in total. So it would anyway be impossible to be sensitive to just one or two events, as I noted above. Nevertheless, if a signal is not seen, one can usually place an upper limit on its size, and that is what CDF did, using the collected information.
Let me give some more details about the histogram: the black points with error bars show the experimental data, binned in 2.5 GeV intervals. The black curve shows the expected background shape and normalization, which was extracted from a data sample devoid of any possible signal contamination. And the red curve shows what a small signal might look like, on top of the background: a bump in the steeply falling distribution. The size of the shown red bump is exactly the one of the signal that CDF may claim to exclude: a larger signal would have hardly been missed.
Conclusions
Once detection efficiency are accounted for, CDF measures that the W to pi-gamma decay has a branching ratio which is smaller than 0.000064 times the one to electron-neutrino pairs, at 95 percent confidence level. Note that by making reference to the well-measured electron-neutrino decay, CDF factors out of the measurement the uncertainty due to the luminosity, which would otherwise affect the measurement with a 6% systematic error.
The result is still about two orders of magnitude above the expected branching fraction for the decay in the standard model. This means that CDF will never be able to actually see a signal. For that, the LHC experiments will be needed, provided that they collect the luminosity that LHC has been designed for. LHC not only should collect 50 times more data in the course of the next decade, but it will collide protons at an energy that makes W boson production an order of magnitude more frequent. Still, the chance that we will actually manage to detect the elusive W decay to pion-photon pairs is not high! Other similar radiative decays may be more accessible to the LHC experiments, however. And if new physics gives a contribution, they might be much more readily accessible...




Comments