
I am interested to explain in simple terms the kinematics of the problem. The speed he reached when he left the starting ramp was, I am told, 125 kilometers per hour. That is about 35 meters per second. It is a simple exercise to compute what is the length of the jump, if we assume that the angle at the start of the parabola is 45 degrees -the angle which, in the absence of friction with air, guarantees the longest jump.
We write the equations for the motion in the horizontal direction (x, describing the length of the jump) and the vertical one (y, describing the height). For the motion along x we have, in the absence of friction,
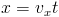
which basically describes a constant-speed motion along x. Along y, on the other hand, we have the gravitational acceleration contributing:
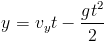
The point where the bike lands can be found by requiring that y=0: this has the obvious solution t=0 (the start of the jump), and the second solution
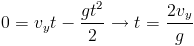
Now we know the time at which the bike lands, so we get the space it traveled along x by susbstituting it in the first equation:
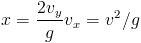
where the last identity is due to the fact that, for a 45° angle of jump, vx and vy are both equal to v divided by the square root of two -they are equal to the sides of a square whose diagonal is v.
If we insert the numbers v=35 m/s and g =10 m/s^2 in the above equation, we find that the jump should have had, in the absence of dissipative forces, a length x=122.5 meters. It was actually shorter, 85 meters, because of the resistence of air; that was not enough to prevent the daring pilot to land safely on the other side of the channel. Remarkable!
Should you ask yourself what was the highest point of the jump (counted with as a reference the ground from which the jump started), it is easy to derive: it correspond to the value of y when the time is half the landing time:
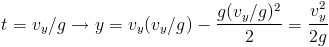
which, with the data in the problem, amounts to about 31 meters. Definitely a WOW jump!



Comments