I may have been unattentive to recent papers on Supersymmetry, but I got the impression that during the last few months the majority of SUSY phenomenologists have been keen on speculating on the few apparently non-standard features of the recently discovered Higgs boson, as published last June (such as the alleged copious decay of photon pairs, or the dearth of decays to tau lepton pairs or b-quark pairs - note: all are mostly back to what the standard model predicts, after the analysis of more data following the discovery announcements), but rather improductive on the front of taking the new signal as a pivot point for new global fits.

The matter is not trivial, although quite important. Inserting the new information in global fits is not trivial because if you want to do things correctly you need to take in account a dozen different rate and limit measurements (which are often moving targets given the pace of new results coming out of LHC and the Tevatron) and reconcile them with the predicted branching fractions that a quintet of non-standard model Higgs bosons may exhibit; with the added trouble that in case more than a single state lies close to 125 GeV they may have been unresolved by the current LHC data, and their branching fractions and relative rates need to be accounted together.

[Incidentally, a true SUSY freak could take the two different mass fits of ATLAS for Higgs decays to photon pairs and Z boson pairs, which lie over two standard deviations apart, and try to interpret them with the existence of two different particles: that would in my humble opinion be too much, but please note that some of us do bet on the fact that these two signals are different resonant states...]

And the matter is of course important because if you believe in Supersymmetry you might want to try and classify the newly found boson at 125 GeV as one of the three neutral states that the less complicated class of SUSY theories predict to exist: two h, H cp-even states, and a CP-odd state A. Or some mixture of those. If you do that, you immediately get some constraining power to add to the many direct searches for SUSY signatures in the tan(β) versus M_A plane. The exercise may thus reveal where to look for the other Higgs bosons, for instance !

So, a new paper by Bechtle, Brein, Heinemeyer, Stal, Stefaniak, Weiglein and Williams describes exactly the above plan, carried out in a software called HiggsSignals, which will be released soon. As a representative exercise, the authors have taken information about experimental rates and limits of neutral Higgs decays in all measured final states by the experiments at the LHC and Tevatron, together with limits from charged Higgs signals, and produced a map of delta-chisquared (a statistical measure of compatibility between experimental results and theoretical predictions) in the tan(β) - A mass plane.

The figure below shows what one should be looking for in the near future if one believes that there are four more Higgs particles there  to discover. In particular, by assuming that the 126-GeV Higgs boson is the heavier of the two neutral CP-even states, then the best-fit region highlighted in black shows that, if one accepts the authors' sample choice of some of the SUSY parameters (except β and M_A), one gets the hint that the A mass is 101 GeV, tan(β) is 6, and the light-Higgs h mass is 92.3 GeV.



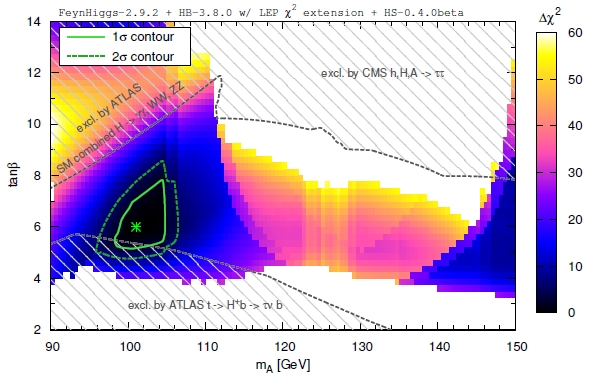
Together with contours of different delta-chisquare the figure shows excluded regions in the plane. These are computed using experimental information complementary to that used for the best-fit point: the upper limits on signal cross section in the various search channels. The window to minimal SUSY is indeed getting narrow! These graphs used to have a vertical scale extending from 0 to 100, and now we are down to ranges of tan(β) from 2 to 14...

Also note that in this scenario the h particle, the lightest Higgs, escapes the LEP II search limits by acquiring reduced couplings to Z bosons (I recall that LEP II limits a standard model Higgs at 114.4 GeV, but that if one assumes that the production cross section of h in electron-positron collisions is smaller than what the standard model calculates, then LEP II could have missed that particle).

I congratulate the authors for this nice new effort, and I look forward to more complete analyses of the SUSY parameter space which take into account all of the information we have amassed on the presence -well on the absence- of Supersymmetry in various parts of the over 100-dimensional space of SUSY theories!